Proof.
Let
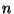
be the order of
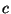
.
In view of the restriction of scalars construction in the proof of
Proposition
1.3, it suffices to show that there is
an extension
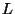
of
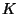
of degree
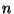
such that
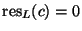
.
Without the hypothesis that
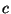
lies in
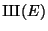
, such an
extension
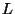
might not exist, as Cassels observed in
[
Cas63]. However, in that
same paper, Cassels proved that such
an
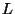
exists when
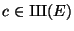
(see also [
O'N01] for another proof).
Let tex2html_wrap_inline$X$ be a genus one curve in the torsor class
corresponding to tex2html_wrap_inline$c$. The long exact sequence associated to
displaymath0&rarr#rightarrow;^0(X_K) &rarr#rightarrow;(X_K)
deg Z&rarr#rightarrow;0begins
displaymath0&rarr#rightarrow;H^0(K,^0(X_K)) &rarr#rightarrow;H^0(K,(X_K))
deg Z &delta#delta; H^1(K,E) &rarr#rightarrow;
&cdots#cdots;,and tex2html_wrap_inline$&delta#delta;(1)=c$ has order tex2html_wrap_inline$n$.
Letting tex2html_wrap_inline$(X_K)$ denote the principal divisors on tex2html_wrap_inline$X_K$,
we have an exact sequence
displaymath0&rarr#rightarrow;(X_K) &rarr#rightarrow;(X_K) &rarr#rightarrow;(X_K)&rarr#rightarrow;0,from which we obtain the exact sequence
displaymath(X) &rarr#rightarrow;H^0(K,(X_K)) &rarr#rightarrow;H^1(K,(X_K)).Since tex2html_wrap_inline$(X_K)=K(X)^*/K^*$,
Hilbert's theorem 90 produces
an injection
displaymathH^1(K,(X_K))&rarrhk#hookrightarrow;H^2(K,K^*)=(K),so
tex2html_wrap_inline$((X)&rarr#rightarrow;H^0(K,(X_K)))$ is
isomorphic to the image of tex2html_wrap_inline$H^0(K,(X_K))$ in tex2html_wrap_inline$(K)$.
Because tex2html_wrap_inline$X$ has a point everywhere locally, this image is locally
zero; hence, by the local-to-global principle for the Brauer
group, this image is globally zero.
In other words, every tex2html_wrap_inline$K$-rational divisor class on tex2html_wrap_inline$X$
contains a tex2html_wrap_inline$K$-rational divisor.
We now show that there is a point on tex2html_wrap_inline$X$ defined over an extension of degree
at most tex2html_wrap_inline$n$. Since tex2html_wrap_inline$n&isin#in;(&delta#delta;)$, there exists tex2html_wrap_inline$D&isin#in;(X)$ which maps
to tex2html_wrap_inline$n &isin#in;Z$ under the degree map.
By the Riemann-Roch theorem, there is an effective divisor linearly
equivalent to tex2html_wrap_inline$D$. Since this divisor is effective and of degree tex2html_wrap_inline$n$,
each point in the support of tex2html_wrap_inline$D$ is defined over an extension tex2html_wrap_inline$L$ of tex2html_wrap_inline$K$of degree at most tex2html_wrap_inline$n$ (alternatively, the residue field of each
scheme-theoretic
point is of degree at most tex2html_wrap_inline$n$). Thus the index of tex2html_wrap_inline$c$ is at most tex2html_wrap_inline$n$(recall that tex2html_wrap_inline$X(L)&ne#neq;&empty#emptyset;$ if and only if tex2html_wrap_inline$_L(c)=0$).
This completes the proof because the order of tex2html_wrap_inline$c$, which is tex2html_wrap_inline$n$,
divides the index of tex2html_wrap_inline$c$, which is at most tex2html_wrap_inline$n$.

Remark 2.5
In contrast to the case of dimension
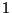
, it seems to be an open
problem to determine whether or not elements of
![$ {\mbox{{\fontencoding{OT2}\fontfamily{wncyr}\fontseries{m}\fontshape{n}\selectfont Sh}}}(A)[n]$](img85.png)
split
over an extension of degree
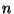
.
![]() lies in
lies in
![]() we use a classical result of Cassels to
strengthen the conclusion of Proposition 2.3.
we use a classical result of Cassels to
strengthen the conclusion of Proposition 2.3.
![]()