Every Element is Visible Somewhere

Proposition 1.3   Every element of $H^1(K,A)$ is visible in some abelian variety $J$.

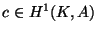
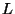
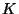
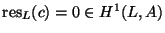
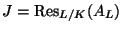
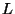
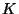
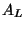
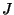
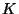
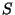
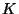
Proof. Fix $c\in H^1(K,A)$. There is a finite separable extension $L$ of $K$ such that $\res_L(c) = 0\in H^1(L,A)$. Let $J=\Res_{L/K}(A_L)$ be the Weil restriction of scalars from $L$ to $K$ of the abelian variety $A_L$ (see [BLR90, §7.6]). Thus $J$ is an abelian variety over $K$ of dimension $[L:K]\cdot \dim(A)$, and for any scheme $S$ over $K$, we have a natural (functorial) group isomorphism $A_L(S_L)\cong {}J(S)$. 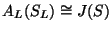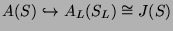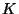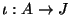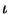The functorial injection $A(S) \hookrightarrow A_L(S_L) \cong {}J(S)$ corresponds via Yoneda's Lemma to a natural $K$-group scheme map $\iota: A\rightarrow J$, and by construction $\iota$ is a monomorphism. 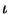But $\iota$ is proper and thus is a closed immersion (see [Gro66, §8.11.5]). 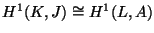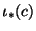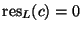Using the Shapiro lemma one finds, after a tedious computation, that there is a canonical isomorphism $H^1(K,J)\cong H^1(L,A)$ which identifies $\iota_*(c)$ with $\res_L(c)=0$. $\qedsymbol$

Remark 1.4  

1. In [CM00], de Jong gave a totally different proof of the above proposition in the case when $A$ is an elliptic curve over a number field. His argument actually displays $A$ as visible inside the Jacobian of a curve.
2. L. Clozel has remarked that the method of proof above is a standard technique in the theory of algebraic groups.