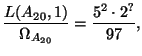Proof.
Let
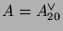
,
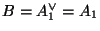
and
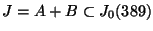
.
Using algorithms in [
AS02],
we find that
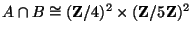
, so
![$ B[5] \subset A$](img237.png)
. Since
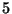
does not divide the
numerator of
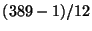
, it does not divide the Tamagawa numbers or
the orders of the torsion subgroups of
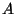
,
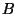
,
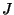
, and
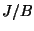
(we also verified this using a modular symbols computations), so
Theorem
3.1 implies that there
is an injective map
To finish, note that Cremona [
Cre97] has verified that
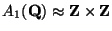
.

![]() .
Using [AS02], we find that
.
Using [AS02], we find that