Next: Restricted Topological Products Up: Global Fields and Adeles Previous: Global Fields and Adeles Contents Index
Below we will focus attention on number fields leaving the function field case to the reader.
The following lemma essentially says that the denominator of an element of a global field is only ``nontrivial'' at a finite number of valuations.
Suppose now that ![]() is a finite extension of
is a finite extension of
![]() , so
, so
![]() satisfies a monic polynomial
satisfies a monic polynomial
Any valuation on a global field is either archimedean, or discrete
non-archimedean with finite residue class field, since this is true of
![]() and
and
![]() and is a property preserved by extending a valuation
to a finite extension of the base field. Hence it makes sense to talk
of normalized valuations. Recall that the normalized
and is a property preserved by extending a valuation
to a finite extension of the base field. Hence it makes sense to talk
of normalized valuations. Recall that the normalized ![]() -adic
valuation on
-adic
valuation on
![]() is
is
![]() , and if
, and if ![]() is a
valuation on a number field
is a
valuation on a number field ![]() equivalent to an extension of
equivalent to an extension of
![]() , then the normalization of
, then the normalization of ![]() is the composite of the
sequence of maps
is the composite of the
sequence of maps
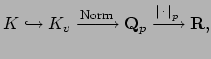
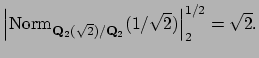
There are two extensions of
![]() to
to
![]() ,
since
,
since
![]() ,
as
,
as
![]() . The image of
. The image of ![]() under each embedding into
under each embedding into
![]() is a unit in
is a unit in
![]() , so
the normalized valuation of
, so
the normalized valuation of
![]() is, in both
cases, equal to
is, in both
cases, equal to ![]() . More generally, for any valuation
of
. More generally, for any valuation
of ![]() of characteristic an odd prime
of characteristic an odd prime ![]() , the
normalized valuation of
, the
normalized valuation of ![]() is
is ![]() .
.
Since
![]() in two ways, there are exactly
two normalized archimedean valuations on
in two ways, there are exactly
two normalized archimedean valuations on ![]() , and
both of their values on
, and
both of their values on ![]() equal
equal
![]() .
Notice that the product of the absolute values of
.
Notice that the product of the absolute values of ![]() with respect to all normalized valuations is
with respect to all normalized valuations is
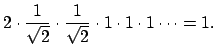

Let ![]() run through all normalized valuations of
run through all normalized valuations of
![]() (or of
(or of
![]() ),
and write
),
and write ![]() if the restriction of
if the restriction of ![]() to
to
![]() is equivalent to
is equivalent to ![]() .
Then by Theorem 19.2.2,
.
Then by Theorem 19.2.2,
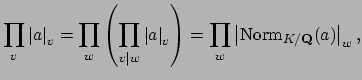
By multiplicativity of valuations, if the theorem is true for ![]() and
and
![]() then it is true for the product
then it is true for the product ![]() and quotient
and quotient ![]() (when
(when
![]() ). The theorem is clearly true for
). The theorem is clearly true for ![]() , which has valuation
, which has valuation
![]() at all valuations. Thus to prove the theorem for
at all valuations. Thus to prove the theorem for
![]() it suffices
to prove it when
it suffices
to prove it when ![]() is a prime number. Then we have
is a prime number. Then we have
![]() ,
,
![]() , and for primes
, and for primes ![]() that
that
![]() . Thus
. Thus
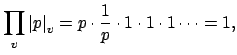
If ![]() is a valuation on a field
is a valuation on a field ![]() , recall that
we let
, recall that
we let ![]() denote the completion of
denote the completion of ![]() with respect to
with respect to ![]() . Also when
. Also when
![]() is non-archimedean, let
is non-archimedean, let
We will use the following lemma later (see Lemma 20.3.3) to prove that formation of the adeles of a global field is compatible with base change.
Since
![]() for all
for all ![]() , the left hand side of
(20.1.2) is contained in the right hand side if
, the left hand side of
(20.1.2) is contained in the right hand side if
![]() for
for
![]() and
and
![]() . Thus by Lemma 20.1.2, for all but finitely many
. Thus by Lemma 20.1.2, for all but finitely many ![]() the left hand side of (20.1.2) is contained in the right
hand side. We have just eliminated the finitely many primes
corresponding to ``denominators'' of some
the left hand side of (20.1.2) is contained in the right
hand side. We have just eliminated the finitely many primes
corresponding to ``denominators'' of some ![]() , and now only
consider
, and now only
consider ![]() such that
such that
![]() for
all
for
all ![]() .
.
For any elements
![]() , consider the
discriminant
, consider the
discriminant
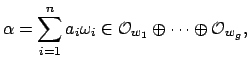
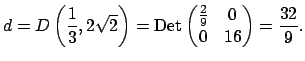
William Stein 2004-05-06