Next: Topology and Completeness Up: Valuations Previous: Types of Valuations Contents Index
There are many non-archimedean valuations. On the rationals
![]() there is one for every prime
there is one for every prime ![]() , the
, the ![]() -adic valuation, as
in Example 15.2.9.
-adic valuation, as
in Example 15.2.9.
http://www-gap.dcs.st-and.ac.uk/~history/Mathematicians/Ostrowski.htmlOstrowski was a Ukrainian mathematician who lived 1893-1986. Gautschi writes about Ostrowski as follows: ``... you are able, on the one hand, to emphasise the abstract and axiomatic side of mathematics, as for example in your theory of general norms, or, on the other hand, to concentrate on the concrete and constructive aspects of mathematics, as in your study of numerical methods, and to do both with equal ease. You delight in finding short and succinct proofs, of which you have given many examples ...'' [italics mine]
Nonarchimedean case:
Suppose
![]() for all
for all
![]() , so by
Lemma 15.2.10,
, so by
Lemma 15.2.10,
![]() is nonarchimedean.
Since
is nonarchimedean.
Since
![]() is nontrivial, the set
is nontrivial, the set
Archimedean case: By replacing
![]() by a power of
by a power of
![]() , we may assume without loss that
, we may assume without loss that
![]() satisfies the
triangle inequality. We first make some general remarks about any
valuation that satisfies the triangle inequality.
Suppose
satisfies the
triangle inequality. We first make some general remarks about any
valuation that satisfies the triangle inequality.
Suppose
![]() is greater than
is greater than ![]() . Consider, for any
. Consider, for any
![]() the base-
the base-![]() expansion of
expansion of ![]() :
:
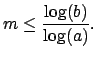
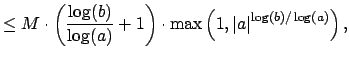 |
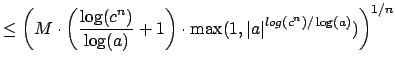 |
||
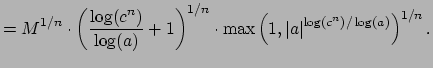 |
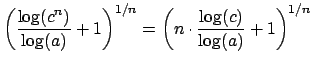
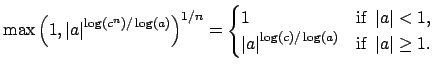
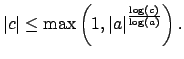
Our assumption that
![]() is nonarchimedean implies
that there is
is nonarchimedean implies
that there is
![]() with
with ![]() and
and
![]() .
Then for all
.
Then for all
![]() with
with ![]() we have
we have
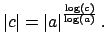
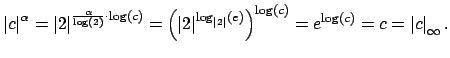
Let ![]() be any field and let
be any field and let ![]() , where
, where ![]() is transcendental. Fix a real number
is transcendental. Fix a real number ![]() .
If
.
If ![]() is an irreducible
polynomial in the ring
is an irreducible
polynomial in the ring ![]() , we define a valuation
by
, we define a valuation
by
This definition differs from the one in [Cas67, pg. 46]
in two ways. First, we assume that ![]() instead of
instead of ![]() , since
otherwise
, since
otherwise
![]() does not satisfy Axiom 3 of a valuation. Here's
why: Recall that Axiom 3 for a non-archimedean valuation on
does not satisfy Axiom 3 of a valuation. Here's
why: Recall that Axiom 3 for a non-archimedean valuation on ![]() asserts that whenever
asserts that whenever ![]() and
and
![]() , then
, then
![]() . Set
. Set ![]() , where
, where
![]() is an
irreducible polynomial. Then
is an
irreducible polynomial. Then
![]() , since
, since
![]() . However,
. However,
![]() , since
, since
![]() . If we take
. If we take ![]() instead of
instead of ![]() , as I propose,
then
, as I propose,
then
![]() , as required.
, as required.
Note the (albeit imperfect) analogy between ![]() and
and
![]() .
If
.
If ![]() , so
, so ![]() , the valuation
, the valuation
![]() is of the type (15.3.3) belonging to the irreducible
polynomial
is of the type (15.3.3) belonging to the irreducible
polynomial ![]() .
.
The reader is urged to prove the following lemma as a homework problem.
William Stein 2004-05-06