Next: Global Fields and Adeles Up: Extensions and Normalizations of Previous: Extensions of Valuations Contents Index
In case (1) we defined the normalized valuation to
be the one such that if Haar measure of the ring of integers ![]() is
is ![]() ,
then
,
then
![]() (see Definition 17.1.11).
In case (2i) we say that
(see Definition 17.1.11).
In case (2i) we say that
![]() is normalized if it is the ordinary
absolute value, and in (2ii) if it is the square of the ordinary
absolute value:
is normalized if it is the ordinary
absolute value, and in (2ii) if it is the square of the ordinary
absolute value:
We have already verified the above characterization for
non-archimedean valuations, and it is clear for the ordinary absolute
value on
![]() , so it remains to verify it for
, so it remains to verify it for
![]() . The additive
group
. The additive
group
![]() is topologically isomorphic to
is topologically isomorphic to
![]() , so a
choice of Haar measure of
, so a
choice of Haar measure of
![]() is the usual area measure on the
Euclidean plane. Multiplication by
is the usual area measure on the
Euclidean plane. Multiplication by
![]() is the same as
rotation followed by scaling by a factor of
is the same as
rotation followed by scaling by a factor of
![]() , so if we
rescale a region by a factor of
, so if we
rescale a region by a factor of ![]() , the area of the region changes
by a factor of the square of
, the area of the region changes
by a factor of the square of
![]() . This explains why the
normalized valuation on
. This explains why the
normalized valuation on
![]() is the square of the usual absolute
value. Note that the normalized valuation on
is the square of the usual absolute
value. Note that the normalized valuation on
![]() does not satisfy
the triangle inequality:
does not satisfy
the triangle inequality:
By the preceding section there is a positive real number ![]() such that for all
such that for all ![]() we have
we have
One can argue in a unified way in all cases as follows.
Let
![]() be a basis for
be a basis for ![]() . Then the map
. Then the map
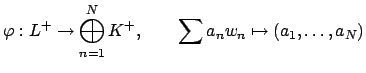
Let ![]() . Then the left-multiplication-by-
. Then the left-multiplication-by-![]() map
map
In the case when ![]() need not be complete with respect
to the valuation
need not be complete with respect
to the valuation
![]() on
on ![]() , we have the following
theorem.
, we have the following
theorem.
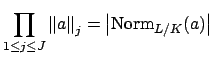
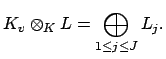
What next?! We'll building up to giving a new proof of finiteness of the class group that uses that the class group naturally has the discrete topology and is the continuous image of a compact group.
William Stein 2004-05-06