Next: The -adic Numbers Up: -adic Numbers Previous: -adic Numbers Contents Index
By unique factorization of integers, there is a smallest multiple ![]() of
of ![]() such that
such that ![]() is exactly divisible by
is exactly divisible by ![]() . Now apply the
above argument with
. Now apply the
above argument with ![]() and
and ![]() replaced by
replaced by ![]() and
and ![]() .
.
![]()
For example,
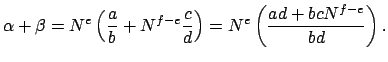
We can finally define the ![]() -adic numbers.
-adic numbers.
William Stein 2004-05-06