The Topology of
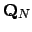 (is Weird)
(is Weird)
Definition 16.2.10 (Connected)
Let
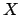
be a topological space. A subset
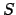
of
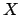
is
if there exist open subsets
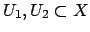
with
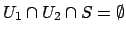
and
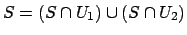
with
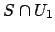
and
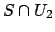
nonempty.
If
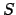
is not disconnected it is
.
The topology on
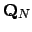 is induced by
is induced by 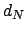 , so every open set is a union
of open balls
, so every open set is a union
of open balls
Recall Proposition 16.2.8, which asserts that for
all 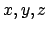 ,
This translates into the following shocking and bizarre lemma:
,
This translates into the following shocking and bizarre lemma:
Proof.
Suppose
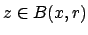
and
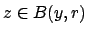
. Then
a contradiction.

You should draw a picture to illustrates Lemma 16.2.11.
Proof.
Suppose
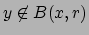
. Then
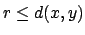
so
Thus the complement of
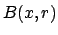
is a union of open balls.

The lemmas imply that
 is ,
in the following sense.
is ,
in the following sense.
Proposition 16.2.13
The only connected subsets of
 are the singleton sets
are the singleton sets
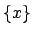 for
for
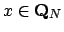 and the empty set.
and the empty set.
Proof.
Suppose
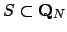
is a nonempty connected set and
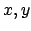
are distinct
elements of
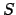
. Let
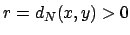
. Let
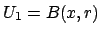
and
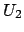
be
the complement of
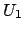
, which is open by Lemma
16.2.12.
Then
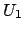
and
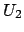
satisfies the conditions of Definition
16.2.10,
so
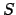
is not connected, a contradiction.

William Stein
2004-05-06
![]() is induced by
is induced by ![]() , so every open set is a union
of open balls
, so every open set is a union
of open balls
![]() is ,
in the following sense.
is ,
in the following sense.