Next: Fermat's Last Theorem in Up: -adic Numbers Previous: The -adic Numbers Contents Index
The ![]() -adic numbers also have decimal expansions, but everything is backward!
To get a feeling for why this might be the case, we consider Euler's
nonsensical series
-adic numbers also have decimal expansions, but everything is backward!
To get a feeling for why this might be the case, we consider Euler's
nonsensical series
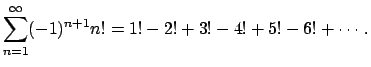
What is ![]() ? How can we write it down? First note that for all
? How can we write it down? First note that for all
![]() , the terms of the sum are divisible by
, the terms of the sum are divisible by ![]() , so the difference
between
, so the difference
between ![]() and
and
![]() is divisible by
is divisible by ![]() . Thus
we can compute
. Thus
we can compute ![]() modulo
modulo ![]() by computing
by computing
![]() modulo
modulo ![]() . Likewise, we can compute
. Likewise, we can compute ![]() modulo
modulo ![]() by compute
by compute
![]() , etc.
We obtain the following table:
, etc.
We obtain the following table:
Here's another example. Reducing ![]() modulo larger and larger powers of
modulo larger and larger powers of ![]() we
see that
we
see that
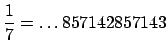 in $Q_10$
in $Q_10$Here's another example, but with a decimal point.
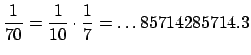
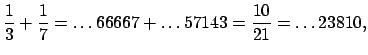
William Stein 2004-05-06