Next: Quadratic Extensions Up: Decomposition and Inertia Groups Previous: Galois Extensions Contents Index
Note that if
![]() and
and ![]() , then
, then ![]() induces an isomorphism of finite fields
induces an isomorphism of finite fields
![]() that fixes the common subfield
that fixes the common subfield
![]() . Thus the residue class
degrees of
. Thus the residue class
degrees of ![]() and
and
![]() are the same. In fact, much more is
true.
are the same. In fact, much more is
true.
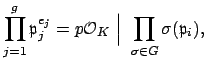
Choose some ![]() and suppose that
and suppose that ![]() is another index. Because
is another index. Because
![]() acts transitively, there exists
acts transitively, there exists
![]() such that
such that
![]() . Applying
. Applying ![]() to the factorization
to the factorization
![]() , we see that
, we see that
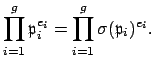
As was mentioned right before the statement of the theorem, for any
![]() we have
we have
![]() , so by transitivity
, so by transitivity
![]() .
Since
.
Since ![]() is a lattice in
is a lattice in ![]() , we have
, we have
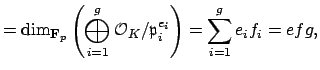 |
The rest of this section illustrates the theorem for quadratic fields and a cubic field and its Galois closure.