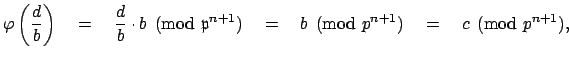Recall that the Chinese Remainder Theorem from elementary number
theory asserts that if
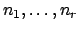 are integers that are coprime
in pairs, and
are integers that are coprime
in pairs, and
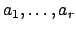 are integers, then there exists an
integer
are integers, then there exists an
integer  such that
such that
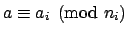 for each
for each
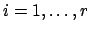 .
In terms of rings, the Chinese Remainder Theorem asserts that the
natural map
is an isomorphism. This result generalizes to rings of integers of
number fields.
.
In terms of rings, the Chinese Remainder Theorem asserts that the
natural map
is an isomorphism. This result generalizes to rings of integers of
number fields.
Proof.
The ideal
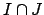
is the largest ideal of

that is divisible
by (contained in) both

and
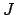
. Since

and
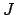
are coprime,
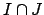
is divisible by
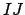
, i.e.,
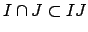
. By
definition of ideal
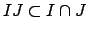
, which
completes the proof.

Remark 9.1.2
This lemma is true for any ring
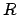
and ideals
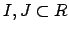
such that
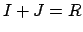
. For the general proof, choose
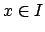
and
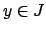
such that
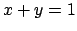
. If
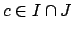
then
so
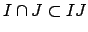
, and the other inclusion is obvious by definition.
Proof.
First assume that we know the theorem in the case when the
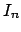
are
powers of prime ideals. Then we can deduce the general case by noting
that each
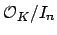
is isomorphic to a product
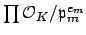
, where
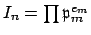
, and
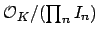
is isomorphic to the product of the
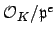
,
where the
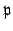
and
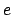
run through the same prime powers as appear
on the right hand side.
It thus suffices to prove that if
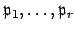 are distinct
prime ideals of
are distinct
prime ideals of  and
and
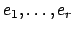 are positive integers,
then
are positive integers,
then
is an isomorphism. Let
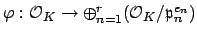
be the natural map induced by reduction mod
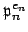
. Then kernel of
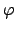
is
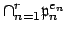
,
which by Lemma
9.1.1 is equal to
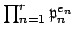
, so
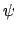
is injective. Note that the projection
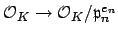
of
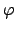
onto each factor is obviously
surjective, so it suffices to show that the element
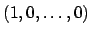
is in the image of
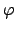
(and the similar elements for the other
factors). Since
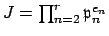
is not divisible
by
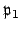
, hence not contained in
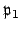
, there is
an element
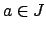
with
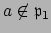
. Since
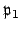
is maximal,
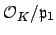
is a field, so there exists
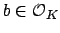
such that
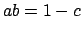
, for some
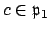
. Then
is congruent to
0 mod
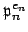
for each
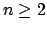
since it is in
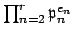
, and it
is congruent to
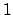
modulo
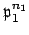
.

Remark 9.1.4
In fact, the surjectivity part of the above proof is easy to prove
for any commutative ring; indeed, the above proof illustrates how
trying to prove something in a special case can result in a more
complicated proof!! Suppose
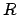
is a ring and
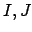
are ideals in
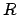
such that
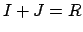
. Choose
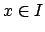
and
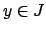
such that
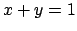
. Then
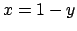
maps to
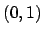
in
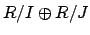
and
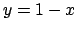
maps to
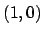
in
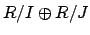
. Thus the map
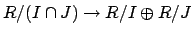
is surjective. Also, as mentioned above,
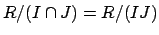
.
Example 9.1.5
The
command
ChineseRemainderTheorem implements the
algorithm suggested by the above theorem. In the following example,
we compute a prime over
and a prime over
of the ring of
integers of
![$ \mathbf{Q}(\sqrt[3]{2})$](img632.png)
, and find an element of

that is
congruent to
![$ \sqrt[3]{2}$](img633.png)
modulo one prime and
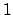
modulo the other.
> R<x> := PolynomialRing(RationalField());
> K<a> := NumberField(x^3-2);
> OK := MaximalOrder(K);
> I := Factorization(3*OK)[1][1];
> J := Factorization(5*OK)[1][1];
> I;
Prime Ideal of OK
Two element generators:
[3, 0, 0]
[4, 1, 0]
> J;
Prime Ideal of OK
Two element generators:
[5, 0, 0]
[7, 1, 0]
> b := ChineseRemainderTheorem(I, J, OK!a, OK!1);
> b - a in I;
true
> b - 1 in J;
true
> K!b;
-4
The element found by the Chinese Remainder Theorem algorithm in
this case is
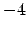
.
The following lemma is a nice application of the Chinese Remainder
Theorem. We will use it to prove that every ideal of  can be
generated by two elements. Suppose
can be
generated by two elements. Suppose  is a nonzero integral ideals of
is a nonzero integral ideals of
 . If
. If 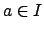 , then
, then
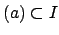 , so
, so  divides
divides 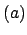 and
the quotient
and
the quotient 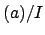 is an integral ideal. The following lemma
asserts that
is an integral ideal. The following lemma
asserts that 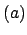 can be chosen so the quotient
can be chosen so the quotient 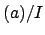 is coprime to
any given ideal.
is coprime to
any given ideal.
Lemma 9.1.6
If 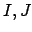 are nonzero integral ideals in
are nonzero integral ideals in  , then there exists
an
, then there exists
an 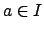 such that
such that 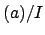 is coprime to
is coprime to 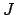 .
.
Proof.
Let
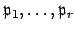
be the prime divisors of
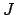
.
For each
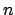
, let
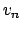
be the largest power of
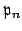
that divides

. Choose an element
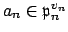
that is not in
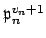
(there is such an element
since
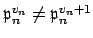
, by unique factorization).
By Theorem
9.1.3, there exists
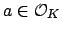
such that
for all
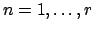
and
also
(We are applying the theorem with the coprime integral ideals
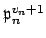
, for
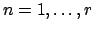
and the integral
ideal
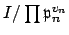
.)
To complete the proof we must show that 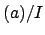 is not
divisible by any
is not
divisible by any
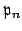 , or equivalently, that the
, or equivalently, that the
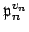 exactly divides
exactly divides 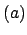 . Because
. Because
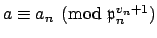 , there is
, there is
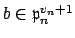 such that
such that
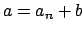 . Since
. Since
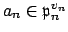 , it follows that
, it follows that
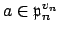 ,
so
,
so
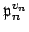 divides
divides 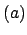 . If
. If
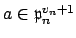 ,
then
,
then
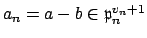 , a contradiction, so
, a contradiction, so
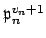 does not divide
does not divide 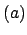 , which completes
the proof.
, which completes
the proof.

Suppose  is a nonzero ideal of
is a nonzero ideal of  . As an abelian group
. As an abelian group  is free of rank equal to the degree
is free of rank equal to the degree
![$ [K:\mathbf{Q}]$](img327.png) of
of  , and
, and  is of
finite index in
is of
finite index in  , so
, so  can be generated as an abelian group,
hence as an ideal, by
can be generated as an abelian group,
hence as an ideal, by
![$ [K:\mathbf{Q}]$](img327.png) generators. The following proposition
asserts something much better, namely that
generators. The following proposition
asserts something much better, namely that  can be generated as an ideal in
can be generated as an ideal in  by at most two elements.
by at most two elements.
Proposition 9.1.7
Suppose  is a fractional ideal in the ring
is a fractional ideal in the ring  of integers of a
number field. Then there exist
of integers of a
number field. Then there exist 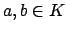 such that
such that 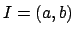 .
.
Proof.
If
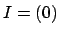
, then

is generated by
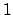
element and we are done. If

is not an integral ideal, then there is
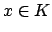
such that
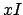
is
an integral ideal, and the number of generators of
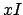
is the same as
the number of generators of

, so we may assume that

is an
integral ideal.
Let  be any nonzero element of the integral ideal
be any nonzero element of the integral ideal  . We will
show that there is some
. We will
show that there is some 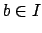 such that
such that 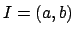 . Let
. Let 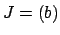 .
By Lemma 9.1.6, there exists
.
By Lemma 9.1.6, there exists 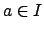 such that
such that 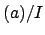 is
coprime to
is
coprime to 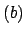 . The ideal
. The ideal
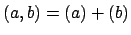 is the greatest common
divisor of
is the greatest common
divisor of 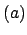 and
and 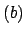 , so
, so  divides
divides 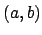 , since
, since  divides
both
divides
both 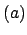 and
and 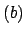 . Suppose
. Suppose
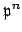 is a prime power that divides
is a prime power that divides
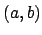 , so
, so
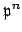 divides both
divides both 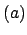 and
and 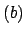 . Because
. Because 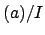 and
and 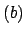 are coprime and
are coprime and
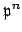 divides
divides 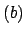 , we see that
, we see that
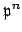 does not divide
does not divide 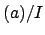 , so
, so
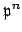 must divide
must divide  . Thus
. Thus 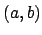 divides
divides  , so
, so 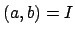 as claimed.
as claimed.

We can also use Theorem 9.1.3 to determine the
 -module structure of the successive quotients
-module structure of the successive quotients
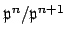 .
.
Proposition 9.1.8
Let
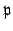 be a nonzero prime ideal of
be a nonzero prime ideal of  , and let
, and let 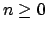 be an
integer. Then
be an
integer. Then
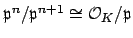 as
as  -modules.
-modules.
Proof.
(Compare page 13 of Swinnerton-Dyer.)
Since
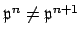
(by unique factorization), we
can fix an element
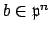
such that
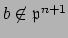
. Let
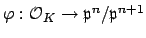
be the

-module morphism defined by
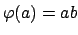
. The kernel of
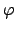
is
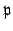
since clearly
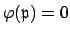
and if
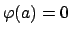
then
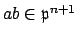
, so
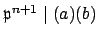
, so
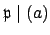
, since
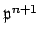
does not
divide
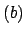
. Thus
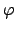
induces an injective

-module
homomorphism
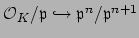
.
It remains to show that 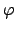 is surjective, and this is where we
will use Theorem 9.1.3. Suppose
is surjective, and this is where we
will use Theorem 9.1.3. Suppose
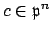 .
By Theorem 9.1.3 there exists
.
By Theorem 9.1.3 there exists
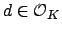 such that
such that

and
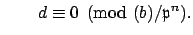
We have
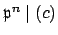
since
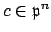
and
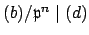
by the second displayed condition, so
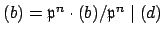
, hence
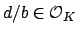
. Finally
so
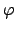
is surjective.

William Stein
2004-05-06
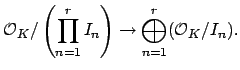
![]() are distinct
prime ideals of
are distinct
prime ideals of ![]() and
and
![]() are positive integers,
then
are positive integers,
then
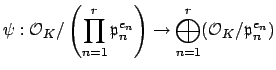
![]() can be
generated by two elements. Suppose
can be
generated by two elements. Suppose ![]() is a nonzero integral ideals of
is a nonzero integral ideals of
![]() . If
. If ![]() , then
, then
![]() , so
, so ![]() divides
divides ![]() and
the quotient
and
the quotient ![]() is an integral ideal. The following lemma
asserts that
is an integral ideal. The following lemma
asserts that ![]() can be chosen so the quotient
can be chosen so the quotient ![]() is coprime to
any given ideal.
is coprime to
any given ideal.
![]() is not
divisible by any
is not
divisible by any
![]() , or equivalently, that the
, or equivalently, that the
![]() exactly divides
exactly divides ![]() . Because
. Because
![]() , there is
, there is
![]() such that
such that
![]() . Since
. Since
![]() , it follows that
, it follows that
![]() ,
so
,
so
![]() divides
divides ![]() . If
. If
![]() ,
then
,
then
![]() , a contradiction, so
, a contradiction, so
![]() does not divide
does not divide ![]() , which completes
the proof.
, which completes
the proof.
![]()
![]() is a nonzero ideal of
is a nonzero ideal of ![]() . As an abelian group
. As an abelian group ![]() is free of rank equal to the degree
is free of rank equal to the degree
![]() of
of ![]() , and
, and ![]() is of
finite index in
is of
finite index in ![]() , so
, so ![]() can be generated as an abelian group,
hence as an ideal, by
can be generated as an abelian group,
hence as an ideal, by
![]() generators. The following proposition
asserts something much better, namely that
generators. The following proposition
asserts something much better, namely that ![]() can be generated as an ideal in
can be generated as an ideal in ![]() by at most two elements.
by at most two elements.
![]() be any nonzero element of the integral ideal
be any nonzero element of the integral ideal ![]() . We will
show that there is some
. We will
show that there is some ![]() such that
such that ![]() . Let
. Let ![]() .
By Lemma 9.1.6, there exists
.
By Lemma 9.1.6, there exists ![]() such that
such that ![]() is
coprime to
is
coprime to ![]() . The ideal
. The ideal
![]() is the greatest common
divisor of
is the greatest common
divisor of ![]() and
and ![]() , so
, so ![]() divides
divides ![]() , since
, since ![]() divides
both
divides
both ![]() and
and ![]() . Suppose
. Suppose
![]() is a prime power that divides
is a prime power that divides
![]() , so
, so
![]() divides both
divides both ![]() and
and ![]() . Because
. Because ![]() and
and ![]() are coprime and
are coprime and
![]() divides
divides ![]() , we see that
, we see that
![]() does not divide
does not divide ![]() , so
, so
![]() must divide
must divide ![]() . Thus
. Thus ![]() divides
divides ![]() , so
, so ![]() as claimed.
as claimed.
![]()
![]() -module structure of the successive quotients
-module structure of the successive quotients
![]() .
.
![]() is surjective, and this is where we
will use Theorem 9.1.3. Suppose
is surjective, and this is where we
will use Theorem 9.1.3. Suppose
![]() .
By Theorem 9.1.3 there exists
.
By Theorem 9.1.3 there exists
![]() such that
such that