In this chapter we will prove the main structure theorem for the group
of units of the ring of integers of a number field. The answer is
remarkably simple: if  has
has 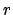 real and
real and 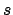 complex embeddings,
then
where
complex embeddings,
then
where 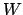 is the finite cyclic group of roots
of unity in
is the finite cyclic group of roots
of unity in  . Examples will follow on Thursday (application:
the solutions to Pell's equation
. Examples will follow on Thursday (application:
the solutions to Pell's equation
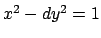 , for
, for 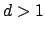 squarefree,
form a free abelian group of rank
squarefree,
form a free abelian group of rank 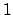 ).
).
Subsections
William Stein
2004-05-06