In the next chapter we will study extra structure in the case when  is Galois over
is Galois over
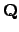 ; the results are nicely algebraic, beautiful, and
have interesting ramifications. We'll learn about Frobenius elements,
the Artin symbol, decomposition groups, and how the Galois group of
; the results are nicely algebraic, beautiful, and
have interesting ramifications. We'll learn about Frobenius elements,
the Artin symbol, decomposition groups, and how the Galois group of
 is related to Galois groups of residue class fields. These are
the basic structures needed to make any sense of representations of
Galois groups, which is at the heart of much of number theory.
is related to Galois groups of residue class fields. These are
the basic structures needed to make any sense of representations of
Galois groups, which is at the heart of much of number theory.
William Stein
2004-05-06