Proof.
We proved before that every ideal class in
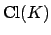
is represented by
an ideal

with
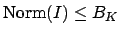
. Write
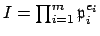
, with each
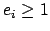
. Then by multiplicativity of the
norm, each
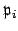
also satisfies
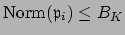
. If
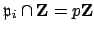
, then

, since
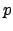
is the residue
characteristic of
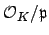
, so
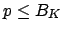
. Thus

is a product of
primes
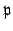
that satisfies the norm bound of the lemma, whcih proves
the lemma.

Example 11.1.2
We compute the class group of
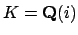
. We have
so
Thus
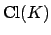
is generated by the prime divisors
of
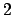
. We have
so
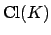
is generated by the principal prime
ideal
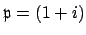
. Thus
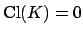
is trivial.
Example 11.1.3
We compute the class group of
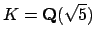
.
We have
so
Thus
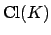
is generated by the primes that divide
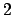
.
We have
![$ \O _K=\mathbf{Z}[\gamma]$](img913.png)
, where
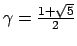
satisfies
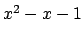
. The polynomial
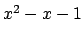
is irreducible
mod
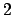
, so
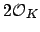
is prime. Since it is principal, we see
that
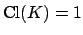
is trivial.
Example 11.1.4
In this example, we compute the class group of
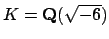
.
We have
so
Thus
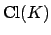
is generated by the prime ideals lying over
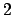
and
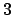
.
We have
![$ \O _K=\mathbf{Z}[\sqrt{-6}]$](img451.png)
, and
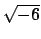
satisfies
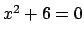
.
Factoring
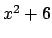
modulo
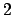
and
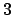
we see that the class group
is generated by the prime ideals
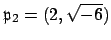
and
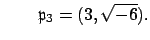
Also,
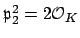
and
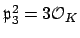
, so
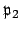
and
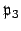
define elements of order
dividing
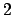
in
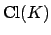
.
Is either
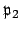 or
or
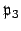 principal? Fortunately,
there is an easier norm trick that allows us to decide.
Suppose
principal? Fortunately,
there is an easier norm trick that allows us to decide.
Suppose
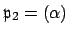 , where
, where
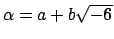 .
Then
.
Then
Trying the first few values of
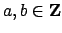
, we see that this
equation has no solutions, so
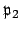
can not
be principal. By a similar argument, we see that
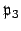
is not principal either. Thus
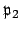
and
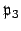
define
elements of order
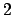
in
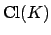
.
Does the class of
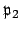 equal the class of
equal the class of
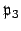 ?
Since
?
Since
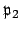 and
and
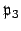 define classes of order
define classes of order 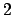 ,
we can decide this by finding the class of
,
we can decide this by finding the class of
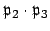 .
We have
.
We have
The ideals on both sides of the inclusion have norm
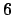
,
so by multiplicativity of the norm, they must be the
same ideal. Thus
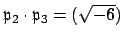
is principal,
so
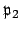
and
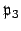
represent the same element of
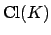
.
We conclude that
![]() :
:
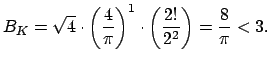
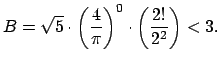
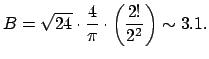
![]() or
or
![]() principal? Fortunately,
there is an easier norm trick that allows us to decide.
Suppose
principal? Fortunately,
there is an easier norm trick that allows us to decide.
Suppose
![]() , where
, where
![]() .
Then
.
Then
![]() equal the class of
equal the class of
![]() ?
Since
?
Since
![]() and
and
![]() define classes of order
define classes of order ![]() ,
we can decide this by finding the class of
,
we can decide this by finding the class of
![]() .
We have
.
We have