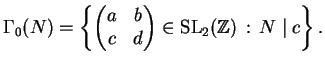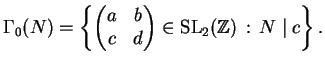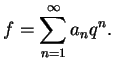Exercise 3.2
Prove that condition 3 is implied by conditions 1 and 2, so condition
3 is redundant. [Hint: Since
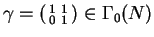
, condition 1 implies that
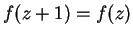
, so there is a function
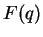
on the open punctured
unit disc such that
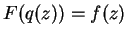
.
Condition 2 implies that
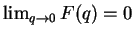
,
so by complex analysis
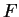
extends to a holomorphic function on the
full open unit disc.]