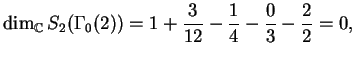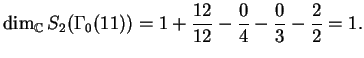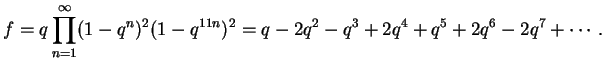Next: Modularity of Elliptic Curves
Up: Cuspidal Modular Forms
Previous: Cuspidal Modular Forms
The Dimension of
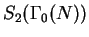
The dimension of
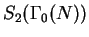 is
where
is
where
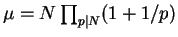 ,
and
,
and
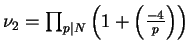 unless
unless 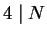 in which case
in which case
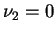 , and
, and
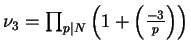 unless
unless 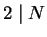 or
or 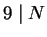 in which case
in which case 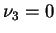 , and
, and
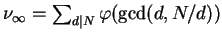 .
For example,
and
One can prove that the vector space
.
For example,
and
One can prove that the vector space
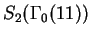 has basis
has basis
Exercise 3.6
Compute the dimension of
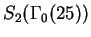
.
William A Stein
2001-11-30
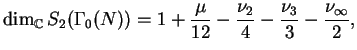
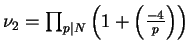 unless
unless 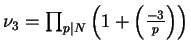 unless
unless