Example 2.1
Let
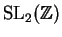
denote the set of
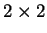
integers matrices
with determinant
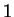
. If
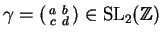
,
then the corresponding
linear fractional transformation
is a holomorphic function on
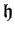
. (Note that the only possible
pole of
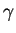
is
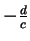
, which is not an element of
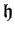
.)
For future use, note that if
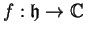 is a holomorphic
function, and
is a holomorphic
function, and
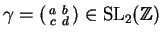 , then
, then
is again a holomorphic function.
Example 2.2
Let
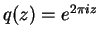
. Then
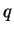
is a holomorphic function
on
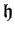
and
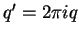
. Moreover,
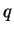
defines a surjective
map from
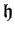
onto the punctured open unit
disk
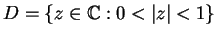
.
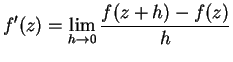
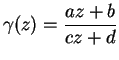
![]() is a holomorphic
function, and
is a holomorphic
function, and
![]() , then
, then