Refinements of results

We now show that parity structures satisfy stronger versions both of the defining condition and of the condition in the definition of a quasi-parity structure. These refinements state not merely that some collection of sets is even, but that when the collection is partitioned in some way according to sizes of the sets involved, every part of the partition contains an even number of sets.

Corollary 2   Let S be any finite set and T be any parity structure for S.

a)

For every odd subset b of S and every even natural number k, there are an even number of subsets of b of size k or k + 1 that lie in T.

b)

For every even subset b of S and every odd natural number k, there are an even number of subsets of b of size k that lie in T.

PROOF:As in the proof of Theorem 2, it suffices to consider the case when T is of the form 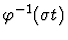 $\varphi^{-1}(\sigma t)$ for some even-degree monomial t. But then parts a) and b) follow from Theorems 1 and 2, respectively, for k equal to the degree of t or this degree plus 1, and they hold trivially for all other values of k. $\Box$

Of course, given the fact that every quasi-parity structure is the symmetric difference of a parity structure and a collection of even sets, it easily follows that quasi-parity structures also satisfy the condition in part b) of Corollary 2.