In order to study parity structures for S, we introduce a ring whose
elements correspond naturally to subsets of
![]() .
Let RS
denote the free (commutative) boolean algebra over
.
Let RS
denote the free (commutative) boolean algebra over
![]() generated
by idempotents corresponding to the elements of S; that is, define
generated
by idempotents corresponding to the elements of S; that is, define
![\begin{displaymath}R_{S}
:= \frac{\mbox{\bf F}_2[x_{s}\, :\, s \in S]}{(x_{s}^{2}- x_{s}\, : \, s \in S)}.
\end{displaymath}](img6.gif)
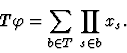
We distinguish the element
![]() of RS; it corresponds under
of RS; it corresponds under ![]() to the collection of subsets
of S of size at most 1. Using RS we obtain a ring-theoretic
characterization of the parity structures for S.
to the collection of subsets
of S of size at most 1. Using RS we obtain a ring-theoretic
characterization of the parity structures for S.
PROOF:Let S have size n, write R for RS, and let P be
the set of all images under ![]() of parity structures for S.
If S is empty, then all subsets of
of parity structures for S.
If S is empty, then all subsets of
![]() are parity structures,
and
are parity structures,
and
![]() generates R as an ideal, so the theorem holds.
Hence we may assume that n is positive.
generates R as an ideal, so the theorem holds.
Hence we may assume that n is positive.
We first translate the set-theoretic condition for the subset T
of
![]() to be a parity structure into an algebraic condition
on
to be a parity structure into an algebraic condition
on ![]() .
For any element t of R and any subset b
of S, write t(b) for the value of the polynomial t with each
indeterminant xs set equal to 1 if s is in b and set
to 0 otherwise. This can be thought of as the evaluation of t on
the characteristic vector of b. For each subset b of S and each
element c of T, the term
.
For any element t of R and any subset b
of S, write t(b) for the value of the polynomial t with each
indeterminant xs set equal to 1 if s is in b and set
to 0 otherwise. This can be thought of as the evaluation of t on
the characteristic vector of b. For each subset b of S and each
element c of T, the term ![]() of
of ![]() will vanish on b
if c is not a subset of b and will give the value 1 otherwise.
Hence
will vanish on b
if c is not a subset of b and will give the value 1 otherwise.
Hence
![]() gives the parity of the number of subsets of b
that lie in T. Therefore, T is a parity structure if and only if,
for every odd subset b of S, the value of
gives the parity of the number of subsets of b
that lie in T. Therefore, T is a parity structure if and only if,
for every odd subset b of S, the value of
![]() is 0.
is 0.
Since polynomial specialization gives ring homomorphisms, for each
odd subset b of S, the map ![]() from R to
from R to
![]() given
by
given
by
![]() is a homomorphism of rings.
And, as the previous remarks show that P is the intersection of the
kernels of these maps for all such subsets b, we see that P is an
ideal of R. Now order the odd subsets of S by increasing size
(with any order chosen for subsets of the same size)
as
is a homomorphism of rings.
And, as the previous remarks show that P is the intersection of the
kernels of these maps for all such subsets b, we see that P is an
ideal of R. Now order the odd subsets of S by increasing size
(with any order chosen for subsets of the same size)
as
![]() .
Then the
.
Then the
![]() matrix with (i,j)-entry equal
to
matrix with (i,j)-entry equal
to
![]() is upper triangular with 1's on the
main diagonal, so the homomorphisms
is upper triangular with 1's on the
main diagonal, so the homomorphisms ![]() are linearly
independent over
are linearly
independent over
![]() .
Hence P has
dimension
2n - 2n-1 = 2n-1 as an
.
Hence P has
dimension
2n - 2n-1 = 2n-1 as an
![]() -vector space.
-vector space.
Next we verify that P contains the ideal I generated
by
![]() .
If b is any odd subset
of S, then b has |b| + 1 subsets of size 0 or 1, and |b| + 1
is even. Hence the collection of subsets of S of size at most 1
is a parity structure, and as the image of this collection under
.
If b is any odd subset
of S, then b has |b| + 1 subsets of size 0 or 1, and |b| + 1
is even. Hence the collection of subsets of S of size at most 1
is a parity structure, and as the image of this collection under ![]() is
is ![]() ,
we have
,
we have
![]() .
Since P is an ideal, it
contains I as a subset.
.
Since P is an ideal, it
contains I as a subset.
Now we show that I and P have the same size, hence must be equal.
Let J be the ideal
![]() .
Notice that
.
Notice that ![]() and
and
![]() are orthogonal idempotents
with sum 1, so R is the direct sum of I and J as rings.
Also, the linear map from R to itself sending xs0
to
1 + xs0 (for some element s0 of S) and fixing xs
for all other values of s is an automorphism of R (since R
can be viewed as the free boolean algebra generated
by
1 + xs0 and the other indeterminants xs).
This automorphism interchanges
are orthogonal idempotents
with sum 1, so R is the direct sum of I and J as rings.
Also, the linear map from R to itself sending xs0
to
1 + xs0 (for some element s0 of S) and fixing xs
for all other values of s is an automorphism of R (since R
can be viewed as the free boolean algebra generated
by
1 + xs0 and the other indeterminants xs).
This automorphism interchanges ![]() and
and
![]() and, hence, also I and J, so I and J have the same dimension
as vector spaces over
and, hence, also I and J, so I and J have the same dimension
as vector spaces over
![]() .
Since their sum R
has dimension 2n, the ideals I and J have dimension 2n-1
over
.
Since their sum R
has dimension 2n, the ideals I and J have dimension 2n-1
over
![]() .
Thus I and P have the same
.
Thus I and P have the same
![]() -dimension,
and since I is a subset of P, they must be equal.
This completes the proof of part (a).
-dimension,
and since I is a subset of P, they must be equal.
This completes the proof of part (a).
Finally, we prove part (b).
For every even-degree monomial t, the product ![]() is the sum of t and some odd-degree monomials, so these products,
with t ranging over all even-degree monomials, are linearly
independent over
is the sum of t and some odd-degree monomials, so these products,
with t ranging over all even-degree monomials, are linearly
independent over
![]() .
But there are 2n-1 such
products, and by the above calculations, the dimension of P
is 2n-1, so the products form a basis for P over
.
But there are 2n-1 such
products, and by the above calculations, the dimension of P
is 2n-1, so the products form a basis for P over
![]() .
This completes the proof of the theorem.
.
This completes the proof of the theorem. ![]()
This result allows us to count immediately the parity structures for a finite set.
PROOF:Theorem 1 shows that the parity structures are in
bijection with an
![]() -vector space of dimension 2n-1.
-vector space of dimension 2n-1. ![]()