


Next: Free boolean algebras and
Up: Parity structures and generating
Previous: Parity structures and generating
We were led to consider parity structures while searching for
a new class of simplicial complexes. We classified parity
structures, but our original proof was based on a
technical induction using binomial coefficients.
Later we found a more conceptual proof that uses
generating functions obtained from a free boolean algebra
over the field
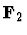 of order 2. In Section 2 we describe
how to view parity structures as elements of this boolean algebra,
and we use this identification to classify parity
structures. We should point out that our classification can be
formulated and proved without this boolean ring with a comparable
amount of work, but we find our method more interesting and more
instructive. In Section 3 we use the classification to find another
property of parity structures. We then prove in Section 4
that parity structures satisfy stronger versions of both the defining
property and this new one. Finally, in Sections 5 and 6 we discuss
some related issues involving an ideal
of order 2. In Section 2 we describe
how to view parity structures as elements of this boolean algebra,
and we use this identification to classify parity
structures. We should point out that our classification can be
formulated and proved without this boolean ring with a comparable
amount of work, but we find our method more interesting and more
instructive. In Section 3 we use the classification to find another
property of parity structures. We then prove in Section 4
that parity structures satisfy stronger versions of both the defining
property and this new one. Finally, in Sections 5 and 6 we discuss
some related issues involving an ideal
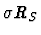 we define below,
and we give a generalization of parity structures.
we define below,
and we give a generalization of parity structures.
William Arthur Stein
1999-10-27