


Next: Visible Elements of
Up: Visibility
Previous: Visibility
Visible Elements of 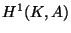
In [Maz99], Mazur introduced the following definition.
Let 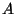 be an abelian variety over an arbitrary field
be an abelian variety over an arbitrary field 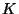 .
.
Definition 1.1
Let
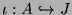
be an embedding of
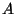
into an abelian variety
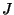
over
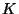
.
Then the
visible subgroup of 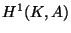 with respect
to the embedding
with respect
to the embedding 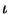
is
The visible subgroup
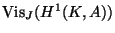 depends on the choice of
embedding
depends on the choice of
embedding 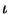 , but we do not include
, but we do not include 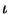 in the notation, as
it is usually clear from context.
in the notation, as
it is usually clear from context.
The Galois cohomology group 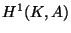 has a geometric interpretation
as the group of classes of torsors
has a geometric interpretation
as the group of classes of torsors 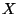 for
for 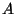 (see [LT58]).
To a cohomology class
(see [LT58]).
To a cohomology class
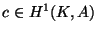 , there is a corresponding
variety
, there is a corresponding
variety 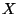 over
over 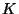 and a map
and a map
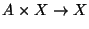 that satisfies axioms
similar to those for a simply transitive group action. The set of
equivalence classes of such
that satisfies axioms
similar to those for a simply transitive group action. The set of
equivalence classes of such 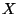 forms a group, the Weil-Chatelet group
of
forms a group, the Weil-Chatelet group
of 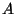 , which is canonically isomorphic to
, which is canonically isomorphic to 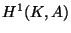 .
.
There is a close relationship between visibility and the geometric
interpretation of Galois cohomology. Suppose
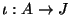 is an
embedding and
is an
embedding and
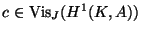 . We have an exact sequence of
abelian varieties
. We have an exact sequence of
abelian varieties
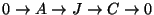 , where
, where 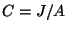 . A piece of
the associated long exact sequence of Galois cohomology is
. A piece of
the associated long exact sequence of Galois cohomology is
so there is an exact sequence
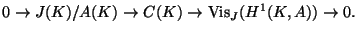 |
(1.1) |
Thus there is a point 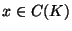 that maps to
that maps to 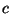 . The fiber
. The fiber 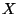 over
over 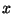 is a subvariety of
is a subvariety of 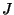 , which, when equipped with its natural
action of
, which, when equipped with its natural
action of 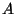 , lies in the class of torsors corresponding to
, lies in the class of torsors corresponding to 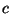 .
This is the origin of the terminology ``visible''. Also, we remark
that when
.
This is the origin of the terminology ``visible''. Also, we remark
that when 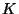 is a number field,
is a number field,
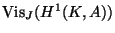 is finite
because it is torsion
and is the surjective image of the finitely generated group
is finite
because it is torsion
and is the surjective image of the finitely generated group 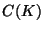 .
.



Next: Visible Elements of
Up: Visibility
Previous: Visibility
William A Stein
2002-02-27
![]() has a geometric interpretation
as the group of classes of torsors
has a geometric interpretation
as the group of classes of torsors ![]() for
for ![]() (see [LT58]).
To a cohomology class
(see [LT58]).
To a cohomology class
![]() , there is a corresponding
variety
, there is a corresponding
variety ![]() over
over ![]() and a map
and a map
![]() that satisfies axioms
similar to those for a simply transitive group action. The set of
equivalence classes of such
that satisfies axioms
similar to those for a simply transitive group action. The set of
equivalence classes of such ![]() forms a group, the Weil-Chatelet group
of
forms a group, the Weil-Chatelet group
of ![]() , which is canonically isomorphic to
, which is canonically isomorphic to ![]() .
.
![]() is an
embedding and
is an
embedding and
![]() . We have an exact sequence of
abelian varieties
. We have an exact sequence of
abelian varieties
![]() , where
, where ![]() . A piece of
the associated long exact sequence of Galois cohomology is
. A piece of
the associated long exact sequence of Galois cohomology is