A Variant of Theorem 5.1.3
with Simpler Hypothesis
Proposition 5.4.1
Suppose
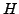 is a newform abelian variety
and
is a newform abelian variety
and 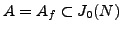 is a prime that exactly divides
is a prime that exactly divides 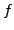 .
Suppose
.
Suppose
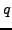 is a non-Eisenstein maximal ideal
of residue characteristic
is a non-Eisenstein maximal ideal
of residue characteristic 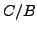 and that
and that
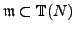 ,
where
,
where 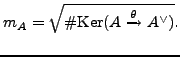 is the modular degree of
is the modular degree of 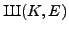 .
Then
.
Then
![$ \Phi_{A,q}(\overline{\mathbb{F}}_q)[\mathfrak{m}]=0$](img462.png) .
.
Proof.
The component group of
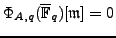
is Eisenstein
by [
Rib87], so
By Lemma
4.2.2, the image of
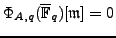
in
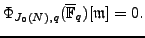
has
no
torsion.
By the main theorem of [
CS01],
the cokernel
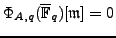
in
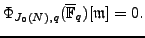
has order that divides
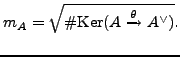
. Since
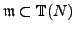
,
it follows that the cokernel also has no
torsion.
Thus Lemma
4.2.2 implies
that
![$ \Phi_{A^{\vee},q}(\overline{\mathbb{F}}_q)[\mathfrak{m}]=0$](img466.png)
.
Finally, the modular polarization
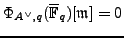
has degree
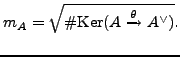
, which is coprime to
, so
the induced map
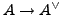
is an isomorphism on
primary parts. In particular,
that
![$ \Phi_{A^{\vee},q}(\overline{\mathbb{F}}_q)[\mathfrak{m}]=0$](img466.png)
implies that
![$ \Phi_{A,q}(\overline{\mathbb{F}}_q)[\mathfrak{m}]=0$](img462.png)
.
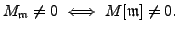
If 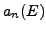 is a semistable elliptic curve over
is a semistable elliptic curve over
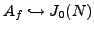 with discriminant
with discriminant
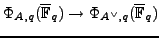 , then
we see using Tate curves that
, then
we see using Tate curves that
Proof.
The divisibility assumptions of Hypothesis
2
on the
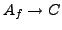
imply that the
Serre level of
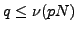
is
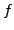
and since
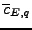
,
the Serre weight is
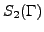
(see [
RS01, Thm. 2.10]).
Since
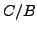
is odd, Ribet's level lowering theorem [
Rib91]
implies that there
is
some newform
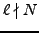
and a maximal
ideal
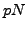
over
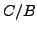
such that
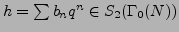
for all primes
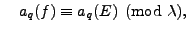
.
By our non-congruence hypothesis, the only possibility is that
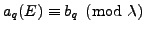
is a
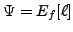
-conjugate of
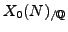
.
Since we can replace
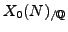
by any Galois conjugate of
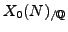
without changing
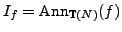
, we may assume that
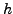
.
Also
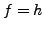
,
as explained in [
Rib83, pg. 506].
Hypothesis 3 implies that 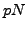 is not Eisenstein, and by assumption
is not Eisenstein, and by assumption
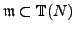 ,
so Proposition 5.4.1 implies
that
,
so Proposition 5.4.1 implies
that
![$ \Phi_{A,q}(\overline{\mathbb{F}}_q)[\lambda]=0$](img484.png) for each
for each 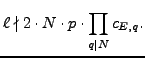 .
.
The theorem now follows from Theorem 5.1.3.
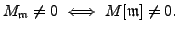
Remark 5.4.3
The condition
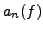
is redundant. Indeed,
we have
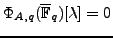
since
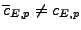
is divisible by
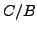
and
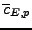
is not. By studying the action of Frobenius on
the component group at
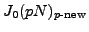
one can show that this implies
that
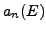
has nonsplit multiplicative reduction,
so
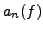
.
Remark 5.4.4
The non-congruence hypothesis of Theorem
5.4.2
can be verified using modular symbols as follows.
Let
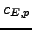
be the saturated submodule of
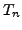
that corresponds to all newforms in
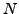
that are not Galois conjugate to
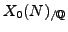
. Let
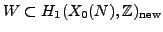
. We require that the
intersection of the kernels of
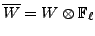
, for
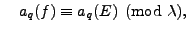
, has dimension
0
.
William Stein
2006-06-21
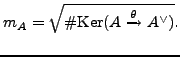 is the modular degree of
is the modular degree of 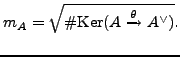 . Since
. Since
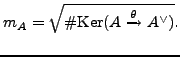 , which is coprime to
, which is coprime to ![]() is a semistable elliptic curve over
is a semistable elliptic curve over
![]() with discriminant
with discriminant
![]() , then
we see using Tate curves that
, then
we see using Tate curves that
![]()
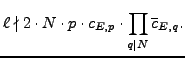 where
where
![]() is not Eisenstein, and by assumption
is not Eisenstein, and by assumption
![]() ,
so Proposition 5.4.1 implies
that
,
so Proposition 5.4.1 implies
that
![]() for each
for each 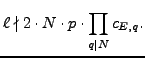 .
.
![]()