Appendix: Some Facts Concerning Toric Reduction

Let $R$ be a discrete valuation ring with fraction field $K$ and residue field $k$. For any abelian variety $A$ over $K$, with Néron model $\mathcal{A}$ over $R$, we denote by $X_A$ the character group of the toric part of $\mathcal{A}^0_k$ (the connected component of the closed fiber of $\mathcal{A}$). All group schemes below are understood to be commutative.

Our aim in this appendix is to prove a couple of facts (Theorem 8.2 and Theorem 8.6) which are no doubt well-known to experts but for which published proofs do not appear to be readily available. We begin with a simple and basic lemma.

Lemma 8.1   Let $f:G \rightarrow G'$ be a map between multiplicative $($resp. étale$)$ finite flat group schemes over $R$. The map $f$ is a closed immersion $($resp. faithfully flat$)$ if and only if the generic fiber map $f_K$ is a closed immersion $($resp. faithfully flat$)$.

Proof. Cartier duality interchanges étaleness and multiplicativeness, as well as closed immersions and faithfully flat maps (as the latter two properties may be checked on the closed fiber, for which one is reduced to the standard case of finite commutative group schemes over a field). Thus, it suffices to consider the étale case. By faithfully flat base change to a strict henselization of $R$, we are reduced to the case where our finite étale group schemes are constant. Since faithful flatness is equivalent to surjectivity (for maps between étale schemes over a base), the lemma is now physically clear.

$\qedsymbol$

Now we turn to the first of the two main results we want to prove. Let $\pi:J \rightarrow {} A$ be an optimal quotient of abelian varieties over $K$ (i.e., we assume that $\ker \pi$ is an abelian variety over $K$), and assume that $J$ has semistable reduction over $R$ (so $A$ does too). We do not yet make any hypotheses of purely toric reduction. The dual abelian varieties $A^{\vee}$ and $J^{\vee}$ again have semistable reduction, as they are isogenous to $A$ and $J$ respectively.

Theorem 8.2   With notation as above, the map $X_{J^{\vee}} \rightarrow X_{A^{\vee}}$ induced by $\pi$ is surjective.

Proof. The underlying idea comes down to two facts: Lemma 8.1 and the fact that we can lift tori on the level of $\ell$-divisible groups for any prime $\ell$. More precisely, we argue as follows. By Proposition 3.3, the map $\pi^{\vee}:A^{\vee} \rightarrow J^{\vee}$ is a closed immersion of abelian varieties. We will use this to prove that the induced map $\pi^{\vee}_t$ on closed fiber tori of Néron models is a closed immersion. Since the ``character group'' functor sets up an anti-equivalence of categories between tori over a field $F$ and finite free $\mathbf{Z}$-modules with continuous action of ${\rm {Gal}}(F_s/F)$, identifying closed immersions of tori with surjections of character groups and surjections of tori with ``saturated injections'' of character groups (i.e., injections with torsion-free cokernel), the closed immersion property for $\pi_t^{\vee}$ on the closed fiber tori will yield the desired surjection of character groups.

In general the ``Néron model'' functor doesn't behave well for closed immersions. That is, just because $\pi^{\vee}$ is a closed immersion, it does not follow purely formally that $\pi^{\vee}$ induces a closed immersion on Néron models. Nevertheless, we claim quite generally that if $B \rightarrow B'$ is a closed immersion of abelian varieties over $K$ with semistable Néron models, then the induced map $T\rightarrow T'$ on closed fiber tori is a closed immersion. For this it is sufficient to prove that the induced map on $\ell$-divisible groups $T[\ell^{\infty}] \rightarrow T'[\ell^{\infty}]$ is a closed immersion for all primes $\ell$ (i.e., all maps $T[\ell^n] \rightarrow T'[\ell^n]$ are closed immersions). Indeed, suppose we verify this closed immersion property on torsion, and let $H$ be the kernel of $T\rightarrow T'$, so $H[\ell^n] = 0$ for all primes $\ell$ and positive integers $n$. The torus $(H^0_{/\overline{k}})_{\rm {red}}$ must vanish (as it has no non-trivial torsion) and hence $H$ is finite. If $N$ is the order of $H$, then $H = H[N] = 0$. The map $T\rightarrow T'$ is then a monomorphism between algebraic groups over a field and hence is a closed immersion, as desired.

In order to verify that the $\ell$-divisible group maps $T[\ell^{\infty}] \rightarrow T'[\ell^{\infty}]$ are closed immersions for all $\ell$, we can make the faithfully flat base change to the henselization of $R$ (which commutes with formation of Néron models) to reduce to the case where $R$ is henselian. Now we recall the following basic result of Grothendieck:

Lemma 8.3   Let $R$ be a henselian local ring, $G$ a quasi-finite separated $R$-scheme of finite presentation. There is a unique decomposition

$$G = G_f \coprod G'$$

into disjoint clopen pieces with $G_f$ finite over $R$ $($called the ``finite part''of $G$$)$ and $G'$ having empty closed fiber. The formation of $G_f$ is functorial in $G$ and is compatible with henselian local base change and formation of fiber products over $R$.

If moreover $G$ is a group scheme over $R$, then $G_f$ is a clopen subgroup scheme and there exists a unique multiplicative closed $R$-subgroup scheme $G_{\mu}$ inside of $G$ whose closed fiber is the multiplicative part of the closed fiber of $G$ $($$G_{\mu}$ is called the ``multiplicative part'' of $G$$)$. The formation of $G_{\mu}$ is functorial in $G$.

Proof. For the first part, see [8, IV$_4$, 18.5.11(c)] (aside from the functorial properties, which are obvious). The second part, concerning group schemes, is a mechanical consequence of the first part (including the functoriality of the finite part). For example, the existence of $G_{\mu}$ follows from considering the connected-étale sequence of the Cartier dual of $G_f$ over the henselian local base $R$, and the uniqueness and functoriality follows from the functoriality of $G \rightsquigarrow G_f$ and the functoriality of the connected-étale sequence.

$\qedsymbol$

Remark 8.4   Assuming $R$ in Lemma 8.3 is a discrete valuation ring (with fraction field $K$ and residue field $k$), let us make some observations concerning the behavior of Lemma 8.3 with respect to primary components, as this will be useful later. Let's suppose that $N$ and $M$ are relatively prime integers with $NM$ divisible by the order of $G_K$, and hence killing $G$. Thus, by functoriality we have $G = G[N] \times_R G[M]$ where $G[N]$ and $G[M]$ are quasi-finite separated $R$-group schemes. We claim that $G[N]$ and $G[M]$ are also flat over $R$, whence it follows that the formation of $G_f$ and $G_{\mu}$ is compatible with passage to ``primary components''.

In other words, if $\ell$ is a prime and $\ell^n$ is divisible by the $\ell$-part of the order of $G_K$, then we claim that $G[\ell^n]$ is $R$-flat. From the clopen decomposition $G = G_f \coprod G'$, it is easy to see that $G[\ell^n] = G_f[\ell^n] \coprod X_n$ for some finite $K$-scheme $X_n$, so for the issue of $R$-flatness we can replace $G$ with $G_f$. We are thereby reduced to the finite flat case, so we can use the proof of [10, 1.7.2].

The significance of Lemma 8.3 for our purposes is the following standard consequence.

Corollary 8.5   Let $A$ be an abelian variety over the fraction field $K$ of a henselian discrete valuation ring $R$ with residue field $k$. Let $\mathcal{A}$ be the Néron model of $A$, and assume that $\mathcal{A}$ has semistable reduction. For every prime $\ell$, there exists a unique multiplicative $\ell$-divisible group $\Gamma_{\ell}$ inside of $\mathcal{A}$ whose closed fiber is the $\ell$-divisible group of the torus $T$ of $\mathcal{A}_k^0$. The formation of $\Gamma_{\ell}$ is functorial in $A$.

Proof. Fix $\ell$. By the semistability hypothesis, the multiplication maps $\ell^n:\mathcal{A}\rightarrow \mathcal{A}$ are quasi-finite flat, so $\mathcal{A}[\ell^n]$ is a quasi-finite flat separated $R$-group scheme. Let $\mathcal{A}[\ell^n]_{\mu}$ denote its multiplicative part (as in Lemma 8.3), so the multiplicative $T[\ell^n] \hookrightarrow \mathcal{A}[\ell^n]_{k}$ lies inside of $(\mathcal{A}[\ell^n]_{\mu})_{k}$. The ``closed fiber'' functor is an equivalence of categories between finite flat multiplicative group schemes over $R$ and $k$ (since Cartier duality reduces this to the étale case, and the ``closed fiber'' functor is an equivalence of categories between finite étale $R$-schemes and finite étale $k$-schemes [8, IV$_4$, 18.5.12]). Thus, there exists a unique multiplicative closed $R$-subgroup scheme $\Gamma^{(n)} \hookrightarrow \mathcal{A}[\ell^n]_{\mu}$ whose closed fiber is $T[\ell^n]$.

Moreover, using the equivalence of categories just mentioned, $\mathcal{A}[\ell^n]_{\mu}$ lies inside of $\mathcal{A}[\ell^{n+1}]_{\mu}$ and $\Gamma^{(n)}$ lies inside of $\Gamma^{(n+1)}$. The resulting system $\Gamma_{\ell} = \{\Gamma^{(n)}\}$ over $R$ forms an $\ell$-divisible group on the closed fiber and hence is an $\ell$-divisible group over $R$. This settles the desired existence, as well as the desired uniqueness. The functoriality of $\Gamma_{\ell}$ in $A$ follows from the functoriality of toric parts on the closed fiber of Néron models.

$\qedsymbol$

Returning to the proof of Theorem 8.2, recall that we were studying the map of toric parts $j_t:T \rightarrow T'$ induced by a closed immersion $j:B \hookrightarrow B'$ of semistable abelian varieties over $K$, with $R$ henselian. We wanted the map

$$j_t[\ell^{\infty}]:T[\ell^{\infty}] \rightarrow T'[\ell^{\infty}]$$

to be a closed immersion for all primes $\ell$ (as we have seen that this forces $T\rightarrow T'$ to be a closed immersion, which is what we really want to show). Fix $\ell$. By Corollary 8.5 there exist unique multiplicative $\ell$-divisible groups $\Gamma$ and $\Gamma'$ over $R$ in the respective Néron models $\mathcal{B}$ and $\mathcal{B}'$ such that $\Gamma$ and $\Gamma'$ respectively lift the $\ell$-divisible groups of the tori of the closed fibers. Hence, it suffices to show that the $R$-map $\gamma: \Gamma \rightarrow \Gamma'$ induced by the Néron functoriality map ${\rm {N}}(j)$ is a closed immersion. The generic fiber map $\gamma_K$ is a closed immersion since it ``sits inside'' the generic fiber $\ell$-divisible groups of $B$ and $B'$, the map between which is a closed immersion since $j:B \rightarrow B'$ is a closed immersion. Now we use Lemma 8.1 (applied at all finite torsion levels) to conclude that $\gamma$ is a closed immersion. This completes the proof of Theorem 8.2.

$\qedsymbol$

We now turn to a result which requires a stronger hypothesis on the closed fiber. Note that we retain the hypothesis that $R$ is henselian (this hypothesis arose in the proof of Theorem 8.2, even though it wasn't needed for the statement). Let $A$ and $B$ be abelian varieties over $K$ with purely toric reduction (i.e., their Néron models have closed fiber connected components which are tori). Let $\varphi :A \rightarrow B$ be an isogeny, and let $\varphi _t:T_A \rightarrow T_B$ be the induced map on the closed fiber toric parts (i.e., connected components) of the Néron models. We denote by $\varphi ^{\vee}_t:T_{B^{\vee}} \rightarrow T_{A^{\vee}}$ the analogous map induced by the dual isogeny $\varphi^{\vee}$. Since the map $\varphi _t$ is an isogeny (by functoriality), the kernel $\ker(\varphi _t)$ is a finite multiplicative $k$-group scheme.

For any finite multiplicative $k$-group scheme $G$, we let $\widetilde{G}$ denote the (unique) multiplicative finite flat $R$-group scheme with closed fiber $G$. For example, $\widetilde{\ker(\varphi _t)}$ is a multiplicative $R$-group scheme which lies inside of

$$\ker({\rm {N}}(\varphi ))_{\mu}$$

(where ${\rm {N}}(\varphi )$ is the map induced by Néron functoriality). Thus, we have a natural closed immersion

$$\widetilde{(\ker \varphi _t)_{K}} \hookrightarrow \ker \varphi$$

and likewise we have a natural quotient map

$$\ker(\varphi^{\vee})^{\vee} \rightarrow \widetilde{\ker(\varphi^{\vee}_t)}_K^{\vee}$$

dual to the natural closed immersion using the isogeny $\varphi^{\vee}$.

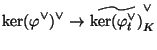
By the duality theory for abelian varieties (particularly the adjointness of $\varphi$ and $\varphi^{\vee}$ with respect to the scheme-theoretic Weil pairing over $K$), there is a canonical perfect duality $K$-group scheme duality between $\ker(\varphi )$ and $\ker(\varphi ^{\vee})$ over $K$, whence there is a natural quotient map of $K$-group schemes

$$\ker(\varphi ) \simeq \ker(\varphi ^{\vee})^{\vee} \rightarrow \widetilde{\ker(\varphi^{\vee}_t)}_K^{\vee}.$$

Theorem 8.6   The diagram of $K$-group schemes

$$0 \rightarrow \widetilde{\ker(\varphi _t)}_K \rightarrow \ker(\varphi ) \rightarrow \widetilde{\ker(\varphi ^{\vee}_t)}^{\vee}_K \rightarrow 0$$

is exact.

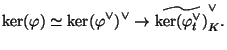
The content of the proof is the Grothendieck Orthogonality Theorem. Moreover, Theorem 8.6 is implicit in Grothendieck's construction of the monodromy pairing for semiabelian varieties.

Proof. The exact sequence of the theorem says that the finite flat $K$-group schemes p

$$\ker(\varphi )/\widetilde{\ker(\varphi _t)}_K$$    and $$\quad \widetilde{\ker(\varphi ^{\vee}_t)}_K$$

are canonically Cartier dual to each other compatibly with the perfect duality between $\ker(\varphi )$ and $\ker(\varphi ^{\vee})$. More precisely, let $\mathcal{A}$ and $\mathcal{B}$ denote the Néron models of $A$ and $B$, respectively, let

$$G = \ker(\mathcal{A}\rightarrow \mathcal{B}), G^{\vee} = \ker(\mathcal{B}^{\vee} \rightarrow \mathcal{A}^{\vee}),$$

so $G$ and $G^{\vee}$ are both quasi-finite flat separated $R$-group schemes whose generic fibers are the $\ker(\varphi )$ and $\ker(\varphi ^{\vee})$ in the theorem (the $R$-flatness of $G$ and $G^{\vee}$ arises from the semiabelian condition, since any quasi-finite morphism between semi-abelian schemes is necessarily flat, as can be checked on geometric fibers). Being quasi-finite flat and separated, the $R$-group schemes $G$ and $G^{\vee}$ have canonical respective ``finite parts'' $G_f$ and $G_f^{\vee}$ and ``multiplicative parts'' $G_{\mu}$ and $G^{\vee}_{\mu}$ (as in Lemma 8.3). Beware that we do not claim $G^{\vee}_f$ (resp. $G^{\vee}_{\mu}$) is the Cartier dual to $G_f$ (resp. $G_{\mu}$); usually such duality does not hold.

Since $G_{\mu}$ and $G^{\vee}_{\mu}$ are finite flat $R$-group schemes, the quotients $G/G_{\mu}$ and $G^{\vee}/G^{\vee}_{\mu}$ make sense as quasi-finite flat separated $R$-group schemes. The theorem almost says that there is a canonical duality between $(G/G_{\mu})_K = G_K/(G_{\mu})_K$ and $(G^{\vee}_{\mu})_K$, induced by the duality between $G_K = \ker(\varphi )$ and $G^{\vee}_K = \ker(\varphi ^{\vee})$, except for the mild problem that $G_{\mu}$ might be larger than $\widetilde{\ker(\varphi _t)}$ (i.e., possibly $(G_{\mu})_{k}$ is not entirely inside of $\mathcal{A}^0_{k}$) and likewise $G^{\vee}_{\mu}$ might be larger than $\widetilde{\ker(\varphi ^{\vee}_t)}$.

We will work on $\ell$-primary components for each prime $\ell$ individually. In order to permit this, we use Remark 8.4. We will first treat the more subtle case when $\ell$ is the residue characteristic, and then we'll handle the case when it isn't. The advantage of working with the case in which $\ell$ is the residue characteristic is that multiplicative finite $k$-group schemes are automatically connected. Thus, in this case $(G_{\mu})_{\ell} = \widetilde{\ker(\varphi _t)}_{\ell}$ and $(G^{\vee}_{\mu})_{\ell} = \widetilde{\ker(\varphi ^{\vee}_t)}_{\ell}$.

Since

$$0 \rightarrow G_K \rightarrow A \rightarrow B \rightarrow 0$$

is an exact sequence of abelian sheaves on the fppf site over $\Spec(K)$, by the usual snake lemma argument (and the fact that the $\ell$-part $(G_K)_\ell$ of $G_K$ is killed by a big power of $\ell$) we obtain an exact sequence

$$0 \rightarrow (G_K)_\ell \rightarrow A[\ell^{\infty}] \rightarrow B[\ell^{\infty}] \rightarrow 0.$$

Arguing as in Corollary 8.5, there is an exact sequence over $\Spec(R)$

$$0 \rightarrow (G_{\mu})_{\ell} \rightarrow \mathcal{A}[\ell^{\infty}]_t \rightarrow \mathcal{B}[\ell^{\infty}]_t \rightarrow 0$$

which lifts the exact sequence involving $\ell$-divisible groups of tori on the closed fiber (as $(G_{\mu})_{\ell}$ must be in the relative connected component of $\mathcal{A}$). Passing to the generic fiber over $K$ gives us a commutative diagram with exact rows and closed immersions along columns

$$\xymatrix{ 0\ar[r] & {((G_{\mu})_K)_{\ell}} \ar[r]\ar[d] & {A[\e... ...G_K)_\ell} \ar[r] & {A[\ell^{\infty}]} \ar[r] & {B[\ell^{\infty}]} \ar[r] & 0 }$$

where $A[\ell^{\infty}]_t$ denotes the $K$-fiber of the $\ell$-divisible group $\{\mathcal{A}[\ell^n]_t\}$, and likewise for $B[\ell^{\infty}]_t$.

Using the snake lemma in the category of fppf abelian sheaves over $\Spec(K)$, we get a short exact sequence of cokernels

$$0 \rightarrow ((G/G_{\mu})_K)_\ell \rightarrow A[\ell^{\infty}]/$$(toric)$$\rightarrow B[\ell^{\infty}]/$$(toric)$$\rightarrow 0$$

where all maps are the natural ones, and right two terms are $\ell$-divisible groups over $K$.

The Grothendieck Orthogonality Theorem (see [9, Exp. IX, Prop 5.6]) asserts that the perfect scheme-theoretic Weil pairing between $A[\ell^n]$ and $A^{\vee}[\ell^n]$ makes $A[\ell^n]_t$ and $A^{\vee}[\ell^n]_f$ exact annhilators, where $A[\ell^n]_f$ denotes the $K$-fiber of the finite part of the $\mathcal{A}^0[\ell^n]$ and $A[\ell^n]_t$ denotes the $K$-fiber of the unique $R$-subgroup scheme in $\mathcal{A}^0[\ell^n]$ lifting the $\ell^n$-torsion on the closed fiber torus. By the purely toric condition applied to $A^{\vee}$, we see $A^{\vee}[\ell^n]_f = A^{\vee}[\ell^n]_t$. Thus, the orthogonality theorem says that $A[\ell^n]/A[\ell^n]_t$ and $A^{\vee}[\ell^n]_t$ are in perfect duality via the scheme-theoretic Weil pairing over $K$.

Passing to the limit, we get a canonical isomorphism of $\ell$-divisible groups

$$A[\ell^{\infty}]/$$(toric)$$= (A^{\vee}[\ell^{\infty}]_t)^{\vee}.$$

But $\varphi$ and $\varphi^{\vee}$ are adjoint with respect to Weil pairing, so we conclude that the diagram

$$\xymatrix{ {A[\ell^{\infty}]/\text{(toric)}} \ar@{=}[r]\ar[d]^{\v... ...l^{\infty}]/\text{(toric)}} \ar@{=}[r] & {(B^{\vee}[\ell^{\infty}]_t)^{\vee}} }$$

commutes. Thus, we get an isomorphism between the kernels of these vertical isogenies. The kernel of the left column is $((G/G_{\mu})_K)_\ell$, as we saw above. Meanwhile, the kernel of the right is (by duality theory of $\ell$-divisible groups) exactly the dual of $\ker(\varphi ^{\vee}_t) = (G^{\vee}_{\mu})_K$. This gives the desired perfect duality between $(G/G_{\mu})_K$ and $(G^{\vee}_{\mu})_K$ on $\ell$-primary parts for $\ell$ equal to the residue characteristic.

Now we consider the case when $\ell$ is not equal to the residue characteristic. There is no loss of generality in passing to the case of a strictly henselian base $R$. Thus, the closed fiber tori have constant $\ell$-divisible groups. Also, we can work with $\mathbf{Z}_\ell$-modules of geometric points (over $K$) via Tate's construction. The ``toric'' part of the $\ell$-adic Tate module $T_{\ell}(A)$ is exactly the (saturated) maximal submodule with trivial Galois action, since a compatible system of $\ell$-power torsion points in $A(K) = \mathcal{A}(R)$ must lie entirely inside of $\mathcal{A}^0(R)$ (thanks to the finiteness of the component group) and we can identify $\mathcal{A}^0(R)[\ell^n]$ with the (constant) $\ell^n$-torsion on the split torus $\mathcal{A}^0_{k}$ over the separably closed $k$.

Using inverse limits, we see that $T_\ell(A) \rightarrow T_\ell(B)$ is injective with cokernel $(G_K)_\ell$ ($=$ geometric points of $\ell$-part), and this cokernel is exactly $\ker(\varphi )_{\ell}$. Likewise, the cokernel of the map

$$T_{\ell}(A)_t \rightarrow T_{\ell}(B)_t$$

on ``toric'' parts (i.e., $\ell$-adic Tate module generic fibers of the lifts of the $\ell$-divisible groups of closed fiber tori) is $(\widetilde{\ker(\varphi _t)}_K)_{\ell}$.

Thus, we get a commutative diagram with horizontal exact sequences

$$\xymatrix{ 0\ar[r] & {T_\ell(A)_t}\ar[r]\ar[d] & {T_\ell(B)_t}\ar... ...r] & {T_\ell(A)}\ar[r] & {T_\ell(B)}\ar[r] & {\ker(\varphi )_\ell}\ar[r] & 0 }$$

with columns given by the natural maps. These vertical maps are all injective, so by the snake lemma we get a short exact sequence of cokernels. We can now use the exact same Weil pairing arguments with the Grothendieck orthogonality theorem (now in the easier `` $\ell \ne p$'' form of the orthogonality theorem [9, Exp IX, 2.4]), essentially just as we argued in the previous case. One distinction is that the use of inverse limit Tate modules rather than direct limits causes some maps to switch direction.

More specifically we have a commutative square with horizontal isomporphisms (thanks to the orthogonality theorem)

$$\xymatrix{ {T_{\ell}(A)/T_{\ell}(A)_t} \ar[d]_-{\varphi} \ar@{=}[... ...e}}\\ {T_{\ell}(B)/T_{\ell}(B)_t} \ar@{=}[r] & {T_{\ell}(B^{\vee})_t^{\vee}} }$$

This induces an isomorphism

$$((\ker \varphi )/\widetilde{\ker(\varphi _t)}_{K})_{\ell} \simeq ((\widetilde{\ker \varphi ^{\vee}_t})_K)_{\ell}^{\vee}$$

between the vertical cokernels, and by construction this isomorphism is compatible with Weil pairings, whence the desired perfect pairing has been shown.

$\qedsymbol$

Let $R$ be an arbitrary dvr (not necessarily henselian), let $\varphi :A \rightarrow B$ be an isogeny, and let $\varphi _t:T_A \rightarrow T_B$ be the induced map on the closed fiber toric parts, as above.

Corollary 8.7   The order of $\ker(\varphi )$ is the product of the orders of $\ker \varphi _t$ and $\ker \varphi ^{\vee}_t$.

Proof. Pass to the henselization of $R$ and use Theorem 8.6. $\qedsymbol$