Next: The Function Field Case Up: Ideles and Ideals Previous: The Idele Group Contents Index
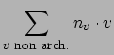
Endow ![]() with the discrete topology. Then there is a natural
continuous map
with the discrete topology. Then there is a natural
continuous map
![]() given by
given by
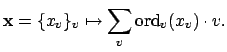

Recall that the ![]() of the number field
of the number field ![]() is by definition the quotient of
is by definition the quotient of ![]() by the image of
by the image of ![]() .
.
Thus the group of ideal classes is the continuous image of the
compact group
![]() (see Theorem 21.1.12), hence
compact. But a compact discrete group is finite.
(see Theorem 21.1.12), hence
compact. But a compact discrete group is finite.
![]()