The invertible elements of any commutative
topological ring 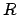 are a group
are a group 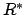 under multiplication.
In general
under multiplication.
In general 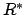 is not a topological group if it is
endowed with the subset topology because inversion need
not be continuous (only multiplication and addition on
is not a topological group if it is
endowed with the subset topology because inversion need
not be continuous (only multiplication and addition on
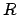 are required to be continuous). It is usual therefore
to give
are required to be continuous). It is usual therefore
to give 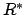 the following topology.
There is an injection
the following topology.
There is an injection
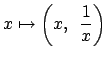 |
(21.1) |
of 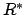 into the topological product
into the topological product 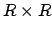 . We give
. We give 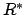 the
corresponding subset topology. Then
the
corresponding subset topology. Then 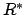 with this topology is a
topological group and the inclusion map
with this topology is a
topological group and the inclusion map
 is continous. To
see continuity of inclusion, note that this topology is finer (has at
least as many open sets) than the subset topology induced by
is continous. To
see continuity of inclusion, note that this topology is finer (has at
least as many open sets) than the subset topology induced by
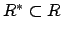 , since the projection maps
, since the projection maps
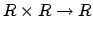 are
continuous.
are
continuous.
Example 21.1.1
This is a ``non-example''. The inverse map on
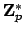
is continuous with
respect to the
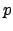
-adic topology. If
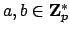
,
then
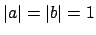
, so if
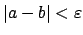
, then
Definition 21.1.2 (Idele Group)
The
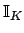
of

is the group
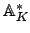
of invertible
elements of the adele ring

.
We shall usually speak of
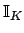 as a subset of
as a subset of  , and will
have to distinguish between the
, and will
have to distinguish between the
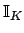 and
and  -topologies.
-topologies.
Example 21.1.3
For a rational prime
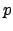
, let
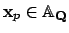
be the adele whose
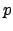
th
component is
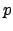
and whose
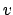
th component, for
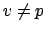
, is
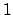
.
Then
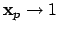
as
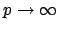
in
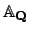
, for the following reason.
We must show that if
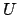
is a basic open set that contains the
adele
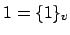
, the
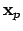
for all sufficiently large
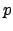
are contained in
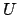
. Since
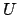
contains
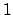
and is a basic
open set, it is of the form
where
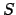
if a finite set, and the
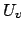
, for
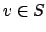
, are
arbitrary open subsets of
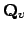
that contain
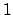
.
If
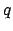
is a prime larger than any prime in
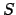
, then
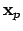
for
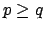
, is in
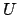
. This proves
convergence.
If the inverse map were continuous on
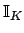
, then
the sequence of
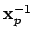
would converge to
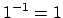
.
However, if
is an open set as above about
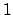
, then
for sufficiently large
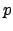
,
none of the adeles
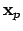
are
contained in
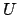
.
Lemma 21.1.4
The group of ideles
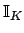 is the restricted topological project
of the
is the restricted topological project
of the 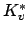 with respect to the units
with respect to the units
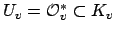 ,
with the restricted product topology.
,
with the restricted product topology.
We omit the proof of Lemma 21.1.4, which is a
matter of thinking carefully about the definitions. The main
point is that inversion is continuous on 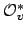 for each
for each 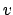 .
(See Example 21.1.1.)
.
(See Example 21.1.1.)
We have seen that  is naturally embedded in
is naturally embedded in  , so
, so
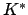 is naturally embedded in
is naturally embedded in
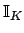 .
.
Definition 21.1.5 (Principal Ideles)
We call
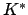
, considered as a subgroup of
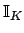
, the
.
Lemma 21.1.6
The principal ideles 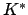 are discrete as a subgroup of
are discrete as a subgroup of
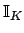 .
.
Proof.
For

is discrete in

, so
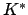
is embedded in
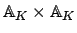
by (
21.1.1) as a discrete subset.
(Alternatively, the subgroup topology on
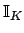
is finer than the
topology coming from
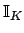
being a subset of

, and

is
already discrete in

.)

Definition 21.1.7 (Content of an Idele)
The
of
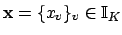
is
Lemma 21.1.8
The map
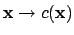 is a continuous homomorphism of
the topological group
is a continuous homomorphism of
the topological group
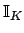 into
into
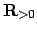 , where
we view
, where
we view
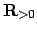 as a topological group under multiplication.
If
as a topological group under multiplication.
If  is a number field, then
is a number field, then 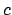 is surjective.
is surjective.
Proof.
That the content map
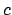
satisfies the axioms of a homomorphisms
follows from the multiplicative nature of the defining formula
for
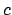
. For continuity, suppose
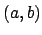
is an open interval
in
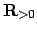
. Suppose
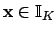
is such that
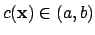
.
By considering small intervals about each non-unit component of
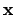
, we find an open neighborhood
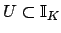
of
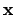
such that
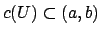
. It follows the
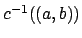
is open.
For surjectivity, use that each archimedean valuation is surjective,
and choose an idele that is 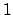 at all but one archimedean valuation.
at all but one archimedean valuation.

Remark 21.1.9
Note also that the
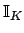
-topology is that appropriate to a
group of operators on
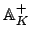
: a basis of open sets
is the
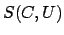
, where
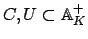
are, respectively,

-compact and

-open, and
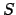
consists of the
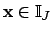
such that
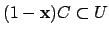
and
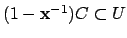
.
Definition 21.1.10 (
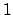
-Ideles)
The subgroup
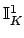
of
is the subgroup of ideles
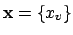
such that
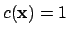
. Thus
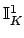
is the kernel of
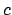
, so we have an exact sequence
where the surjectivity on the right is only if

is a number field.
Lemma 21.1.11
The subset
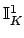 of
of  is closed as a subset,
and the
is closed as a subset,
and the  -subset topology on
-subset topology on
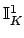 coincides
with the
coincides
with the
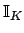 -subset topology on
-subset topology on
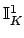 .
.
Proof.
Let
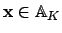
with
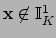
. To prove that
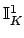
is closed in

, we find an

-neighborhood
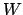
of
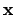
that does not meet
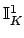
.
1st Case. Suppose that
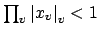 (possibly
(possibly 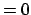 ).
Then there is a finite set
).
Then there is a finite set 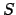 of
of 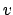 such that
such that
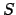 contains all the
contains all the 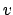 with
with
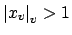 , and
, and
-
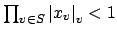 .
.
Then the set
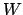
can be
defined by
for sufficiently small
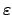
.
2nd Case. Suppose that
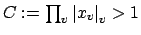 .
Then there is a finite set
.
Then there is a finite set 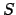 of
of 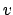 such that
such that
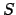 contains all the
contains all the 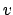 with
with
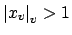 , and
, and
- if
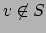 an inequality
an inequality
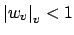 implies
implies
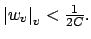 (This is because for a non-archimedean valuation, the
largest absolute value less than
(This is because for a non-archimedean valuation, the
largest absolute value less than 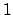 is
is 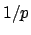 , where
, where 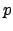 is
the residue characteristic. Also, the upper bound in
Cassels's article is
is
the residue characteristic. Also, the upper bound in
Cassels's article is
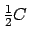 instead of
instead of
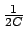 ,
but I think he got it wrong.)
,
but I think he got it wrong.)
We can choose
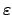
so small that
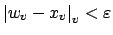
(for
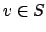
) implies
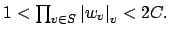
Then
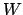
may be defined
by
This works because if
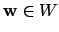
, then either
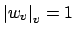
for all
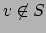
, in
which case
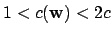
, so
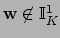
,
or
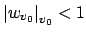
for some
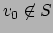
, in
which case
so again
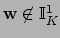
.
We next show that the
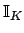 - and
- and  -topologies on
-topologies on
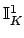 are the same. If
are the same. If
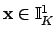 , we must show that every
, we must show that every
 -neighborhood of
-neighborhood of
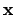 contains an
contains an  -neighborhood
and vice-versa.
-neighborhood
and vice-versa.
Let
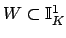 be an
be an  -neighborhood of
-neighborhood of
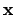 . Then it
contains an
. Then it
contains an  -neighborhood of the type
-neighborhood of the type
where
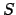
is a finite set of valuations
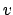
. This contains
the
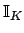
-neighborhood in which
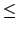
in (
21.1.2)
is replaced by
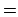
.
Next let
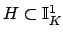 be an
be an
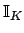 -neighborhood. Then it contains
an
-neighborhood. Then it contains
an
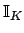 -neighborhood of the form
-neighborhood of the form
where the finite set
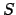
contains at least all archimedean
valuations
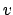
and all valuations
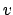
with
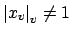
. Since
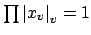
, we may also
suppose that
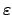
is so small that (
21.1.4)
implies
Then the intersection of (
21.1.4) with
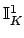
is the same as that of (
21.1.2)
with
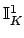
, i.e., (
21.1.4)
defines an

-neighborhood.

By the product formula we have that
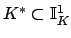 .
The following result is of vital importance in class
field theory.
.
The following result is of vital importance in class
field theory.
Proof.
After the preceeding lemma, it is enough to find
an

-compact set
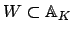
such that the map
is surjective. We take for
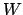
the set of
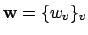
with
where
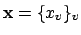
is any idele of content greater than
the
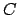
of Lemma
20.4.1.
Let
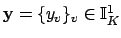 . Then the content of
. Then the content of
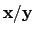 equals
the content of
equals
the content of
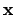 , so by Lemma 20.4.1
there is an
, so by Lemma 20.4.1
there is an 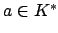 such that
such that
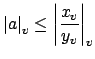
all $v$
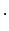
Then
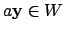
, as required.

Remark 21.1.13
The quotient
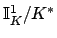
is totally disconnected in the function
field case. For the structure of its connected component in the
number field case, see papers of Artin and Weil in the ``Proceedings
of the Tokyo Symposium on Algebraic Number Theory, 1955'' (Science
Council of Japan) or [
AT90]. The determination of the
character group of
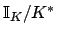
is global class field theory.
William Stein
2004-05-06
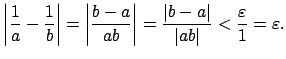
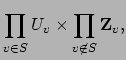
![]() is naturally embedded in
is naturally embedded in ![]() , so
, so
![]() is naturally embedded in
is naturally embedded in
![]() .
.
![]() at all but one archimedean valuation.
at all but one archimedean valuation.
![]()
![]() (possibly
(possibly ![]() ).
Then there is a finite set
).
Then there is a finite set ![]() of
of ![]() such that
such that
![]() .
Then there is a finite set
.
Then there is a finite set ![]() of
of ![]() such that
such that
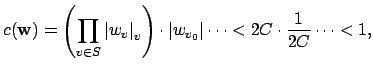
![]() - and
- and ![]() -topologies on
-topologies on
![]() are the same. If
are the same. If
![]() , we must show that every
, we must show that every
![]() -neighborhood of
-neighborhood of
![]() contains an
contains an ![]() -neighborhood
and vice-versa.
-neighborhood
and vice-versa.
![]() be an
be an ![]() -neighborhood of
-neighborhood of
![]() . Then it
contains an
. Then it
contains an ![]() -neighborhood of the type
-neighborhood of the type
![]() be an
be an
![]() -neighborhood. Then it contains
an
-neighborhood. Then it contains
an
![]() -neighborhood of the form
-neighborhood of the form
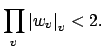
![]() .
The following result is of vital importance in class
field theory.
.
The following result is of vital importance in class
field theory.
![]() . Then the content of
. Then the content of
![]() equals
the content of
equals
the content of
![]() , so by Lemma 20.4.1
there is an
, so by Lemma 20.4.1
there is an ![]() such that
such that
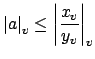 all $v$
all $v$