Proof.
Let
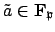
be an element such that
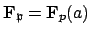
.
Lift
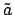
to an algebraic integer
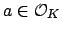
, and let
![$ f=\prod_{\sigma\in D_p}(x-\sigma(a))\in K^D[x]$](img1342.png)
be the characteristic polynomial of

over
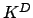
.
Using Proposition
14.1.4 we see that
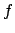
reduces to the minimal polynomial
![$ \tilde{f}=\prod (x-\tilde{\sigma(a)})\in \mathbf{F}_p[x]$](img1343.png)
of
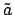
(by the Proposition the coefficients of
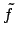
are in
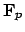
, and
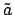
satisfies
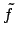
, and the
degree of
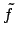
equals the degree of the minimal polynomial
of
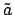
). The roots of
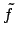
are of the form
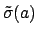
, and
the element
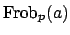
is also a root of
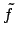
, so it is of the form
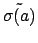
.
We conclude that the generator
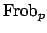
of
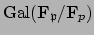
is
in the image of
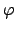
, which proves the theorem.

Proof.
By definition
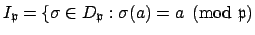 for all
for all 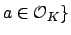
,
so it suffices to show that if
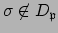
, then there
exists
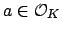
such that
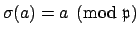
.
If
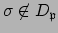
, we have
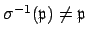
, so
since both are maximal ideals, there exists
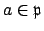
with
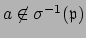
,
i.e.,
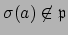
. Thus
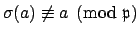
.

![$\displaystyle \char93 D_\mathfrak{p}= [K:L] = \frac{[K:\mathbf{Q}]}{g} = \frac{efg}{g} = ef.$](img1352.png)
![]() .
.
![]() .
.