Galois groups of finite fields
Each
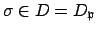 acts in a well-defined
way on the finite field
acts in a well-defined
way on the finite field
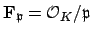 , so we obtain
a homomorphism
We pause for a moment and derive a few basic properties of
, so we obtain
a homomorphism
We pause for a moment and derive a few basic properties of
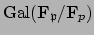 ,
which are in fact general properties of Galois groups for finite fields.
Let
,
which are in fact general properties of Galois groups for finite fields.
Let
![$ f=[\mathbf{F}_\mathfrak{p}:\mathbf{F}_p]$](img1325.png) .
.
The group
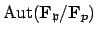 contains the element
contains the element 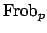 defined by
defined by
because
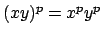 and
By Exercise 29 (see Chapter 22), the group
and
By Exercise 29 (see Chapter 22), the group
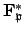 is cyclic, so there is an element
is cyclic, so there is an element
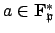 of order
of order
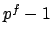 , and
, and
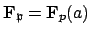 . Then
. Then
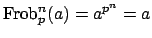 if
and only if
if
and only if
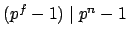 which is the case preciselywhen
which is the case preciselywhen
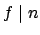 , so the order of
, so the order of 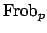 is
is 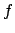 . Since the order of the
automorphism group of a field extension is at most the degree of the
extension, we conclude that
. Since the order of the
automorphism group of a field extension is at most the degree of the
extension, we conclude that
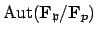 is generated by
is generated by 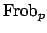 . Also,
since
. Also,
since
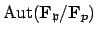 has order equal to the degree, we conclude that
has order equal to the degree, we conclude that
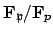 is Galois, with group
is Galois, with group
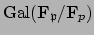 cyclic of order
cyclic of order 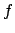 generated by
generated by 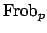 . (Anther general fact: Up to isomorphism
there is exactly one finite field of each degree. Indeed, if there
were two of degree
. (Anther general fact: Up to isomorphism
there is exactly one finite field of each degree. Indeed, if there
were two of degree 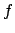 , then both could be characterized as the set of
roots in the compositum of
, then both could be characterized as the set of
roots in the compositum of 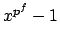 , hence they would be equal.)
, hence they would be equal.)
William Stein
2004-05-06
![]() contains the element
contains the element ![]() defined by
defined by