In this section we extend the notion of norm to ideals. This will be
helpful in proving of class groups in the next section. For example,
we will prove that the group of fractional ideals modulo principal
fractional ideals of a number field is finite by showing that every
ideal is equivalent to an ideal with norm at most some a priori bound.
Definition 10.3.1 (Lattice Index)
If
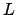
and
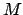
are two lattices in vector space
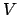
, then the
![$ [L:M]$](img765.png)
is by definition the absolute value of the
determinant of any linear automorphism

of
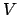
such that
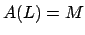
.
The lattice index has the
following properties:
- If
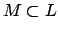 , then
, then
![$ [L:M]=\char93 (L/M)$](img768.png) .
.
- If
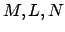 are lattices then
are lattices then
![$ [L:N] = [L:M]\cdot [M:N]$](img770.png) .
.
Definition 10.3.2 (Norm of Fractional Ideal)
Suppose

is a fractional ideal of

. The
of

is
the lattice index
or
0 if
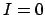
.
Note that if  is an integral ideal, then
is an integral ideal, then
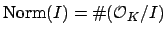 .
.
Proof.
By properties of the lattice index mentioned above we have
Here we have used that
![$ [I:aI]=\vert\Norm _{K/\mathbf{Q}}(a)\vert$](img776.png)
, which is because left
multiplication
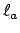
is an automorphism of

that sends

onto
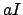
, so
![$ [I:aI]=\vert{\mathrm{Det}}(\ell_a)\vert=\vert\Norm _{K/\mathbf{Q}}(a)\vert$](img777.png)
.

Proposition 10.3.4
If  and
and 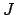 are fractional ideals, then
are fractional ideals, then
Proof.
By Lemma
10.3.3, it suffices to prove this when

and
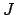
are
integral ideals. If

and
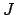
are coprime, then
Theorem
9.1.3 (Chinese Remainder Theorem) implies that

. Thus we reduce to the case when
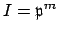
and
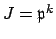
for some prime ideal
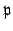
and integers
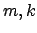
.
By Proposition
9.1.8 (consequence of CRT that
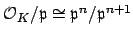
), the filtration of
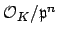
given
by powers of
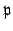
has successive quotients isomorphic to
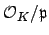
, so
we see that
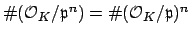
, which proves that
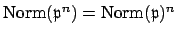
.

Lemma 10.3.5
Fix a number field  .
Let
.
Let  be a positive integer. There
are only finitely many integral ideals
be a positive integer. There
are only finitely many integral ideals
 of
of  with norm at most
with norm at most  .
.
Proof.
An integral ideal

is a subgroup of

of index equal to the
norm of

. If
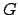
is any finitely generated abelian group, then
there are only finitely many subgroups of
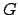
of index at most

,
since the subgroups of index dividing an integer
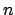
are all subgroups
of
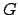
that contain
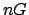
, and the group
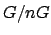
is finite. This
proves the lemma.

William Stein
2004-05-06