Modular symbols are a beautiful piece of mathematics that was
developed since the 1960s by Birch, Manin, Shokorov, Mazur, Merel,
Cremona, and others. Not only are modular symbols a powerful
computational tool as we will see, they have also been used to
prove rationality results for special values of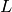 
-series,
to construct 
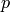-adic 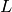-series, and they play a
key role in Merel’s proof of the uniform boundedness theorem for
torsion points on elliptic curves over number fields.
We view modular symbols as a remarkably flexible computational tool
that provides a single uniform algorithm for computing
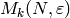for any 
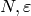and
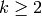. There are ways to use computation of those
spaces to obtain explicit basis for spaces of weight 
and half-integral weight, so in a sense modular symbols yield
everything. There are also generalizations of modular symbols to
higher rank groups, though Sage currently has no code for modular
symbols on higher rank groups.
A modular symbol of weight
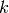, and level 
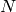, with character 
is a sum of terms 
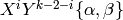, where
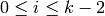and
.
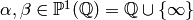Modular symbols satisfy the relations
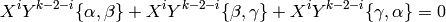
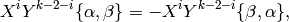
and for every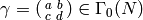 
, we
have
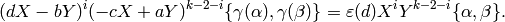
The modular symbols space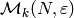 
is the torsion free ![\mathbb{Q}[\varepsilon]](_images/math/717f50dc03bfa3354addba1a71e5a25a969967b6.png)
-module generated by
all sums of modular symbols, modulo the relations listed above.
Here is the ring generated by the values
of the character , so it is of the form
![\mathbb{Q}[\zeta_m]](_images/math/ff320fece7eab7312d089ed9bd00111b7e54dceb.png)
for some integer 
.
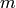The amazing theorem that makes modular symbols useful is that there
is an explicit description of an action of a Hecke algebra
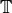on 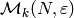, and there is an
isomorphism
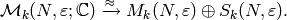
This means that if modular symbols are
computable (they are!), then they can be used to compute a lot
about the 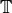-module .
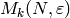Though 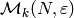as described above is not explicitly
generated by finitely many elements, it is finitely generated. Manin,
Shokoruv, and Merel give an explicit description of finitely many
generators (Manin symbols) for this space, along with all explicit
relations that these generators satisfy (see my book). In particular,
if we let
![(i,c,d) = [X^i Y^{2-k-i}, (c,d)] =
(dX - bY)^i (-cX + aY)^{k-2-i} \{\gamma(0),\gamma(\infty)\},](_images/math/0228399ff7ac2c211b81f23d964137ce12b286b3.png)
where
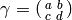, then the Manin symbols
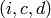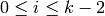with and
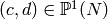generate .
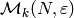We compute a basis for the space
of weight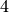 
modular symbols for 
,
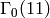then coerce in 
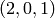and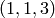 
.
sage: M = ModularSymbols(11,4)
sage: M.basis()
([X^2,(0,1)], [X^2,(1,6)], [X^2,(1,7)], [X^2,(1,8)],
[X^2,(1,9)], [X^2,(1,10)])
sage: M( (2,0,1) )
[X^2,(0,1)]
sage: M( (1,1,3) )
2/7*[X^2,(1,6)] + 1/14*[X^2,(1,7)] - 4/7*[X^2,(1,8)]
+ 3/14*[X^2,(1,10)]
We compute a modular symbols representation for the Manin symbol
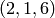, and verify this by converting back.
sage: a = M.1; a
[X^2,(1,6)]
sage: a.modular_symbol_rep()
36*X^2*{5/6,1} - 60*X*Y*{5/6,1} + 25*Y^2*{5/6,1}
sage: 36*M([2,5/6,1]) - 60*M([1,5/6,1]) + 25*M([0,5/6,1])
[X^2,(1,6)]