The Mestre Method of Graphs is an intriguing
algorithm for computing the action of Hecke operators on yet
another module 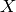 that is isomorphic to
that is isomorphic to
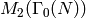 . The implementation in Sage
unfortunately only works when
. The implementation in Sage
unfortunately only works when 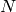 is prime; in contrast, my
implementation in Magma works when
is prime; in contrast, my
implementation in Magma works when 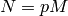 and
and
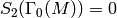 .
.
The matrices of Hecke operators on 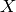 are vastly sparser
than on any basis of
are vastly sparser
than on any basis of 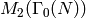 that you are
likely to use.
that you are
likely to use.
sage: X = SupersingularModule(389); X
Module of supersingular points on X_0(1)/F_389 over Integer Ring
sage: t2 = X.T(2).matrix(); t2[0]
(1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0)
sage: factor(charpoly(t2))
(x - 3) * (x + 2) * (x^2 - 2) * (x^3 - 4*x - 2) * ...
sage: t2 = ModularSymbols(389,sign=1).hecke_matrix(2); t2[0]
(3, 0, -1, 0, 0, -1, 1, 0, 0, 0, -1, 1, 0, 1, -1, 0, 1, 1,
0, 1, -1, 1, -1, 1, 0, 0, 0, 0, 0, 0, 1, -1, -1)
sage: factor(charpoly(t2))
(x - 3) * (x + 2) * (x^2 - 2) * (x^3 - 4*x - 2) * ...
The method of graphs is also used in computer science to construct expander graphs with good properties. And it is important in my algorithm for computing Tamagawa numbers of purely toric modular abelian varieties. This algorithm is not implemented in Sage yet, since it is only interesting in the case of non-prime level, as it turns out.