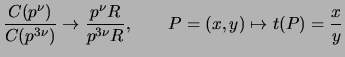Next: About this document ...
Up: Freshman Seminar 21n: Elliptic
Previous: Reading Assignment
Try all the problems but definitely do the ones with your name in
front of them.
- (Mauro)
Look at Figure 2.6 in Silverman-Tate. It is the graph of an elliptic
curve with one real component along with the corresponding graph in the
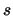 -
-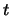 plane. Choose an elliptic curve with two real components
and draw its graph in the
plane. Choose an elliptic curve with two real components
and draw its graph in the 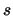 -
-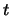 plane.
plane.
- (Alex)
The third paragraph on page 52 of Silverman-Tate begins: ``Let
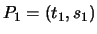 and
and
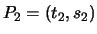 be distinct points. If
be distinct points. If 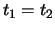 , then
, then 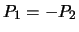 ,
so
,
so 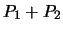 is certainly in
is certainly in
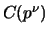 '' (i.e., the
'' (i.e., the 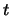 -coordinate of
the sum is divisible by
-coordinate of
the sum is divisible by 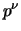 ). I think this is a mistake in the proof,
because
). I think this is a mistake in the proof,
because 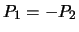 if and only if
if and only if 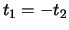 and
and 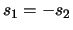 , as discussed
at the bottom of page 53. Repair the mistake; that is, give a proof that
if
, as discussed
at the bottom of page 53. Repair the mistake; that is, give a proof that
if 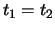 then
then 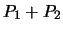 is in
is in
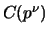 .
.
- (Jeff)
Let
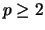 be a prime and let
be a prime and let 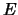 be the elliptic curve
Find all points of finite order in
be the elliptic curve
Find all points of finite order in
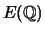 .
.
- (Jenna)
Let
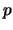 be a prime and let
be a prime and let
![$ S=S_p={\mathbb{Z}}[\frac{1}{p}]$](img19.png) be the set of rational numbers
of the form
be the set of rational numbers
of the form 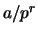 for
for
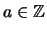 and
and 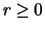 .
.
- Prove that
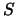 is a subring of
is a subring of
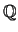 .
.
- Prove that the group of units in
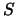 is
is
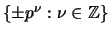 .
.
- Let
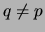 be a prime. Prove that
be a prime. Prove that 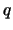 generates a maximal
ideal of
generates a maximal
ideal of 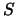 and describe the quotient field
and describe the quotient field 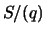 . Prove
that every maximal ideal of
. Prove
that every maximal ideal of 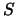 is of this form.
is of this form.
- (Jennifer)
For each of the following elliptic curves
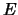 , determine the
torsion subgroup of
, determine the
torsion subgroup of
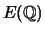 .
You may use the stronger form of Nagell-Lutz (i.e.,
.
You may use the stronger form of Nagell-Lutz (i.e., 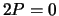 or
or 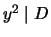 )
and you may use a computer to automate use of
Nagell-Lutz (but don't just write
TorsionSubgroup(EllipticCurve(...)) in MAGMA).
By Mazur's theorem, the groups you get will represent all possibilities for
)
and you may use a computer to automate use of
Nagell-Lutz (but don't just write
TorsionSubgroup(EllipticCurve(...)) in MAGMA).
By Mazur's theorem, the groups you get will represent all possibilities for
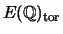 for any elliptic curve
for any elliptic curve 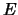 over
over
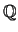 .
.
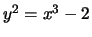
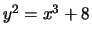
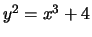
-
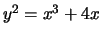
-
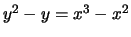
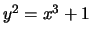
-
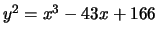
-
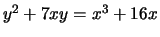
-
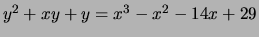
-
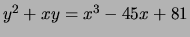
-
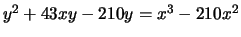
-
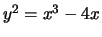
-
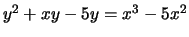
-
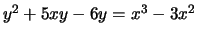
-
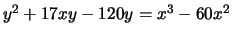
> function t(e) return Invariants(TorsionSubgroup(EllipticCurve(e))); end function;
> t([0,-2]);
> t([0,8]);
[ 2 ]
> t([0,4]);
[ 3 ]
> t([4,0]);
[ 4 ]
> t([0,-1,-1,0,0]);
[ 5 ]
> t([0,1]);
[ 6 ]
> t([-43,166]);
[ 7 ]
> t([7,0,0,16,0]);
[ 8 ]
> t([1,-1,1,-14,29]);
[ 9 ]
> t([1,0,0,-45,81]);
[ 10 ]
> t([43,-210,-210,0,0]);
[ 12 ]
> t([-4,0]);
[ 2, 2 ]
> t([1,-5,-5,0,0]);
[ 2, 4 ]
> t([5,-3,-6,0,0]);
[ 2, 6 ]
> t([17,-60,-120,0,0]);
[ 2, 8 ]
- (Mauro)Use mwrank to find generators for a subgroup
of finite index of the group of rational points on
the following elliptic curves:
-
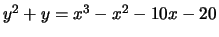
-
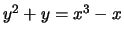
-
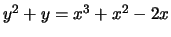
-
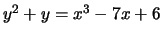
-
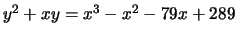
-
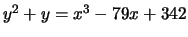
- (Jenna)Use gp (PARI) to do the following elliptic curve arithmetic.
Let
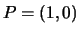 and
and 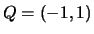 on
on
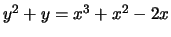 .
.
- Compute
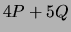 .
.
- Find the smallest multiple
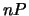 of
of 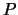 such that
the
such that
the 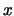 and
and 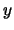 -coordinates of
-coordinates of 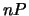 are not both integers, and hence
prove that
are not both integers, and hence
prove that 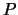 has infinite order. Do the same for
has infinite order. Do the same for 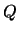 .
.
- Find five distinct right triangles with rational side lengths
and area
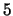 using arithmetic on an elliptic curve and Proposition
4.2 and Example 4.4 from the notes for 02/11/03. Use Nagell-Lutz
to prove that
there are infinitely many right triangles with rational side
lengths and area
using arithmetic on an elliptic curve and Proposition
4.2 and Example 4.4 from the notes for 02/11/03. Use Nagell-Lutz
to prove that
there are infinitely many right triangles with rational side
lengths and area 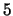 (assuming the truth of Proposition 4.2).
(assuming the truth of Proposition 4.2).
- (Alex)
Use magma to do the same arithmetic as in Exercise 7.
- (Jennifer)
Part (c) of the proposition on page 55 asserts that the map
is a one-to-one homomorphism.
Let
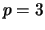 and
and 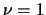 . Determine the size of the image of
this map for the first 3 curves in Problem 6
(assume that the subgroup of finite index output by
mwrank is actually of index
. Determine the size of the image of
this map for the first 3 curves in Problem 6
(assume that the subgroup of finite index output by
mwrank is actually of index 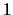 ).
).
- (Jeff)
Prove that for every rational number
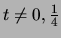 , the
point
, the
point 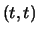 on the elliptic curve defined by
is a point of order four. (See the discussion on page 57 of
[Silverman-Tate], and feel free to use a computer to simplify
the algebra.)
on the elliptic curve defined by
is a point of order four. (See the discussion on page 57 of
[Silverman-Tate], and feel free to use a computer to simplify
the algebra.)



Next: About this document ...
Up: Freshman Seminar 21n: Elliptic
Previous: Reading Assignment
William A Stein
2003-02-24
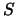 is a subring of
is a subring of
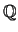 .
.
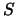 is
is
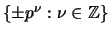 .
.
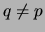 be a prime. Prove that
be a prime. Prove that 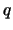 generates a maximal
ideal of
generates a maximal
ideal of 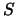 and describe the quotient field
and describe the quotient field 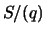 . Prove
that every maximal ideal of
. Prove
that every maximal ideal of 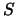 is of this form.
is of this form.
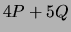 .
.
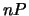 of
of 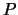 such that
the
such that
the 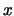 and
and 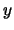 -coordinates of
-coordinates of 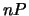 are not both integers, and hence
prove that
are not both integers, and hence
prove that 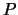 has infinite order. Do the same for
has infinite order. Do the same for 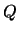 .
.
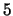 using arithmetic on an elliptic curve and Proposition
4.2 and Example 4.4 from the notes for 02/11/03. Use Nagell-Lutz
to prove that
there are infinitely many right triangles with rational side
lengths and area
using arithmetic on an elliptic curve and Proposition
4.2 and Example 4.4 from the notes for 02/11/03. Use Nagell-Lutz
to prove that
there are infinitely many right triangles with rational side
lengths and area 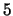 (assuming the truth of Proposition 4.2).
(assuming the truth of Proposition 4.2).