


Next: About this document ...
Up: Freshman Seminar 21n: Elliptic
Previous: Problems for next time.
Definition 4.1 (Congruent Number)
A rational number
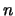
is called a
congruent number if
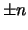
is the area of a right triangle with rational
side lengths. Equivalently,
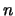
is congruent if the
system of two equations
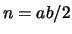
and
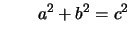
has a solution with
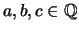
.
For example, 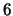 is the area of the right triangle with side lengths
is the area of the right triangle with side lengths 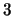 ,
, 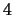 ,
and
,
and 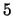 , so
, so 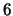 is a congruent number. Less obvious is that
is a congruent number. Less obvious is that 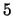 is also a congruent number; it is the area of the right triangle
with side lengths
is also a congruent number; it is the area of the right triangle
with side lengths 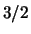 ,
, 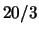 , and
, and 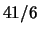 . It is nontrivial
to prove that
. It is nontrivial
to prove that 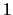 ,
, 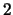 ,
, 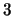 , and
, and 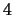 are not congruent numbers.
are not congruent numbers.
Here is a list of the congruent numbers up to 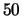 :
:
Every congruence class modulo 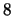 except
except 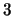 is represented in this list, which
suggests that if
is represented in this list, which
suggests that if
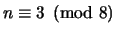 then
then 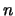 is not a congruent number.
This is true for
is not a congruent number.
This is true for 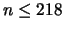 , but
, but 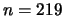 is a congruent number congruent to
is a congruent number congruent to 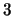 mod
mod 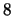 . Something very subtle is going on.
. Something very subtle is going on.
This is another example which hints at the subtlety of congruent numbers. The
number 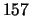 is a congruent number, and Don
Zagier showed that the simplest rational
right triangle with area
is a congruent number, and Don
Zagier showed that the simplest rational
right triangle with area 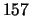 has side lengths
has side lengths
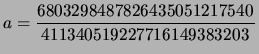
and
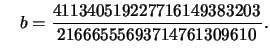
This solution would take a long time to find without understanding
more about congruent numbers.
Open Problem:
Give an algorithm which, given 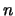 , outputs whether or
not
, outputs whether or
not 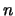 is a congruent number.
is a congruent number.
The following proposition establishes a link between elliptic curves and the
congruent number problem. This link connects the congruent number problem with
the Birch and Swinnerton-Dyer conjecture, which some consider to be the most
important open problem in the theory of elliptic curves.
Proposition 4.2
Let
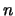
be a rational number.
There is a bijection between
and
given explicitly by the maps
and
Corollary 4.3
The rational number
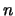
is a congruent number if and only if
the elliptic curve
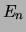
defined by
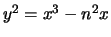
has a solution with
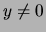
.
Proof.
The number
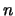
is a congruent number if and only if the set
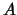
from
Proposition
4.2 is nonempty. By the proposition
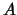
is
nonempty if and only if
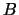
is nonempty, which proves the corollary.

Example 4.4
Let
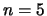
. Then
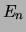
is defined by
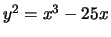
, and we find by a
brute force search the solution
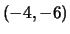
. Then
Multiplying through by
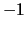
yields the side lengths of a rational
right triangle with area
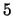
.
Theorem 4.5
Let
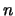
be
even and squarefree, and let
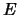
be
the elliptic curve
Then
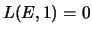
if and only if
So far I have told you nothing about the meaning of ``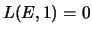 ''.
Suffice for now to know that (a consequence of) the Birch and
Swinnerton-Dyer conjecture is the assertion that the set of rational
solutions to
''.
Suffice for now to know that (a consequence of) the Birch and
Swinnerton-Dyer conjecture is the assertion that the set of rational
solutions to
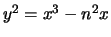 is infinite if and only if ``
is infinite if and only if ``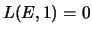 ''.
Also, it is easy to prove that this set of solutions is infinite if
and only if
''.
Also, it is easy to prove that this set of solutions is infinite if
and only if 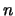 is a congruent number.
is a congruent number.
When 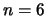 , we get
, we get
When 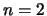 , we get
, we get
so the BSD conjecture predicts that
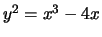 has
no interesting solutions and
has
no interesting solutions and 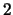 is not a triangle number.
is not a triangle number.
In fact, this is true. The implication
 implies
implies
 has no interesting solutions was proved by Coates and Wiles
(this is the same Wiles who proved Fermat's Last Theorem).
has no interesting solutions was proved by Coates and Wiles
(this is the same Wiles who proved Fermat's Last Theorem).
The other implication:
has lots of solutions
is a fascinating open problem.



Next: About this document ...
Up: Freshman Seminar 21n: Elliptic
Previous: Problems for next time.
William A Stein
2003-02-11
![]() :
:
![]() is a congruent number, and Don
Zagier showed that the simplest rational
right triangle with area
is a congruent number, and Don
Zagier showed that the simplest rational
right triangle with area ![]() has side lengths
has side lengths
 and
and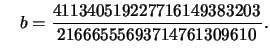
![]() , outputs whether or
not
, outputs whether or
not ![]() is a congruent number.
is a congruent number.
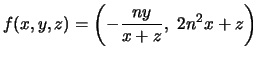
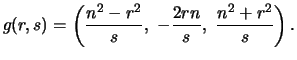
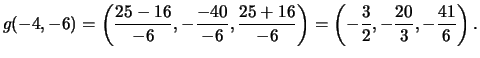
![]() , we get
, we get
![]() , we get
, we get
![]() implies
implies
![]() has no interesting solutions was proved by Coates and Wiles
(this is the same Wiles who proved Fermat's Last Theorem).
has no interesting solutions was proved by Coates and Wiles
(this is the same Wiles who proved Fermat's Last Theorem).