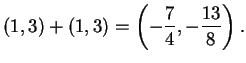Next: About this document ...
Up: Lecture 27: Torsion Points
Previous: The Rank
The following theorem yields an algorithm to compute
 .
.
Theorem 3.1 (Nagell-Lutz)
Suppose that
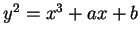
(with
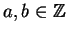
) defines an elliptic
curve
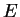
over
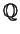
, let
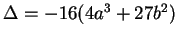
be the discriminant,
and suppose
that
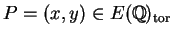
. Then
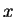
and
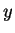
are integers and
either
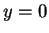
, in which case
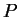
has order
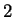
, or
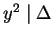
.
Proof.
[Non-proof]
I will not prove this theorem. However, you can find a readable
proof in Chapter II of Silverman and Tate's
Rational Points on Elliptic Curves.

Warning:
Nagell-Lutz is NOT an if and only if statement. There are
points of infinite order that satisfy the conclusion
of Theorem 3.1.
For example, the point 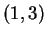 on
on
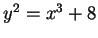 has integer coordinates
and
has integer coordinates
and
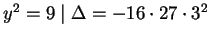 . However,
. However,
Since the coordinates of
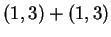 are not integers, it
follows from the contrapositive (not converse!) of
Nagell-Lutz that
are not integers, it
follows from the contrapositive (not converse!) of
Nagell-Lutz that 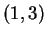 must be a point of infinite order.
must be a point of infinite order.
Example 3.2
The following is a list of elliptic curves with each possible torsion
subgroup. Tom Womack (a graduate student in Nottingham, where Robin
Hood lives) has a web page,
http://www.tom.womack.net/maths/torsion.htm,
which contains PARI code that lists infinitely many elliptic
curve with each torsion subgroup.
The elltors function in PARI computes torsion subgroups:
? ?elltors
elltors(e,{flag=0}): torsion subgroup of elliptic curve e: order, structure,
generators. If flag = 0, use Doud's algorithm; if flag = 1, use Lutz-Nagell.
? e=ellinit([17,-60,-120,0,0]);
? elltors(e)
%4 = [16, [8, 2], [[30, -90], [-40, 400]]]
? e.disc
%5 = 51438240000
? e.disc % 90^2 \\ verify Nagell-Lutz
%6 = 0
? e.disc % 400^2 \\ verify Nagell-Lutz
%7 = 0



Next: About this document ...
Up: Lecture 27: Torsion Points
Previous: The Rank
William A Stein
2001-11-16
![]() on
on
![]() has integer coordinates
and
has integer coordinates
and
![]() . However,
. However,