The main theorem

Let $A_{/K}$ , $B_{/K}$ , $C_{/K}$ , $Q_{/K}$ , $N$ and $\ell$ be as above. Let $R$ be a commutative subring of ${\mathrm{End}}_K(C)$ that leaves $A$ and $B$ stable and let $\mathfrak{m}$ be a maximal ideal of $R$ of residue characteristic $\ell$ . By the Néron mapping property, the subgroups $\Phi_{A, v}(k_v)$ and $\Phi_{B, v}(k_v)$ of $k_v$ -points of the corresponding component groups can be viewed as $R$ -modules.

Theorem 4.1.1 (Equivariant Visibility Theorem)   Suppose that $A(K)$ has rank zero and that the groups $Q(K)[\mathfrak{m}]$ , $B(K)[\mathfrak{m}]$ , $\Phi_{A,v}(k_v)[\mathfrak{m}]$ and $\Phi_{B,v}(k_v)[\ell]$ are all trivial for all nonarchimedean places $v$ of $K$ . Then there is an injective homomorphism of $R/\mathfrak{m}$ -vector spaces

$$(B(K)/\ell{}B(K))[\mathfrak{m}]\hookrightarrow {\mathrm{Vis}}_C({... ...family{wncyr}\fontseries{m}\fontshape{n}\selectfont Sh}}}(K, A))[\mathfrak{m}].$$ (1)

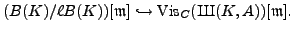
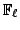
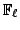
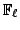
Remark 4.1.2   Applying the above result for $R=\mathbb{Z}$ , we recover the result of Agashe and Stein in the case when $A(K)$ has Mordell-Weil rank zero. We could relax the hypothesis that $A(K)$ is finite and instead give a bound on the dimension of the kernel of (1) in terms of the rank of $A(K)$ similar to the bound in [AS02, Thm. 3.1]. We will not need this stronger result in our paper.