Next: Visible Subgroups of Shafarevich-Tate Up: current Previous: Organization of the paper
1. Abelian varieties. For a number field ![]() ,
, ![]() denotes an abelian variety over
denotes an abelian variety over ![]() .
We denote the dual of
.
We denote the dual of ![]() by
by
![]() . If
. If
![]() is an isogeny of degree
is an isogeny of degree ![]() , we denote the
complementary isogeny by
, we denote the
complementary isogeny by ![]() ; this is the isogeny
; this is the isogeny
![]() , such that
, such that
![]() , the multiplication-by-
, the multiplication-by-![]() map on
map on ![]() . Unless otherwise specified,
Néron models of abelian varieties will be denoted by the corresponding caligraphic letters, e.g.,
. Unless otherwise specified,
Néron models of abelian varieties will be denoted by the corresponding caligraphic letters, e.g.,
![]() denotes
the Néron model of
denotes
the Néron model of ![]() .
.
2. Galois cohomology.
For a fixed algebraic closure
![]() of
of ![]() ,
, ![]() will be the Galois group
will be the Galois group
![]() . If
. If ![]() is any non-archimedean place of
is any non-archimedean place of ![]() ,
, ![]() and
and ![]() will always mean the completion
and the residue field of
will always mean the completion
and the residue field of ![]() at
at ![]() , respectively. By
, respectively. By
![]() we always mean the maximal unramified extension
of the completion
we always mean the maximal unramified extension
of the completion ![]() . Given a
. Given a ![]() -module
-module ![]() , we let
, we let
![]() denote the
Galois cohomology group
denote the
Galois cohomology group
![]() .
.
3. Component groups. The component group of ![]() at
at ![]() is
the finite group
is
the finite group
![]() which also has a structure of a finite
group scheme over
which also has a structure of a finite
group scheme over ![]() . The Tamagawa number of
. The Tamagawa number of ![]() at
at ![]() is
is
![]() , and the component group order of
, and the component group order of ![]() at
at ![]() is
is
![]() .
.
4. Modular abelian varieties. Let ![]() or
or ![]() . A
. A ![]() -modular abelian variety
is an abelian variety
-modular abelian variety
is an abelian variety ![]() which is a quotient of
which is a quotient of ![]() for some
for some ![]() , i.e., there exists a surjective
morphism
, i.e., there exists a surjective
morphism
![]() defined over
defined over ![]() . We define the level of a modular abelian variety
. We define the level of a modular abelian variety
![]() to be the minimal
to be the minimal ![]() , such that
, such that ![]() is a quotient of
is a quotient of ![]() . The modularity theorem of Wiles et al.
(see [BCDT01]) implies that all elliptic curves over
. The modularity theorem of Wiles et al.
(see [BCDT01]) implies that all elliptic curves over
![]() are modular.
Serre's modularity conjecture implies that the modular abelian varieties over
are modular.
Serre's modularity conjecture implies that the modular abelian varieties over
![]() are precisely
the abelian varieties over
are precisely
the abelian varieties over
![]() of
of
![]() -type (see [Rib92, §4]).
-type (see [Rib92, §4]).
5. Shimura construction.
Let
![]() be a newform of level
be a newform of level ![]() and weight 2 for
and weight 2 for
 which is an eigenform for all Hecke operators in the Hecke algebra
which is an eigenform for all Hecke operators in the Hecke algebra
![]() . Shimura
(see [Shi94, Thm. 7.14]) associated to
. Shimura
(see [Shi94, Thm. 7.14]) associated to ![]() an abelian subvariety
an abelian subvariety
![]() of
of ![]() , simple
over
, simple
over
![]() , of dimension
, of dimension
![]() , where
, where
![]() is the Hecke eigenvalue field. More
precisely, if
is the Hecke eigenvalue field. More
precisely, if
![]() then
then ![]() is the connected component containing the identity of the
is the connected component containing the identity of the ![]() -torsion
subgroup of
-torsion
subgroup of ![]() , i.e.,
, i.e.,
![]() . The quotient
. The quotient
![]() of the Hecke algebra
of the Hecke algebra
![]() is a subalgebra of the
endomorphism ring
is a subalgebra of the
endomorphism ring
![]() . Also
. Also
![]() , where the
, where the 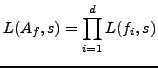 are the
are the
![]() -conjugates of
-conjugates of ![]() . We also consider the dual abelian variety
. We also consider the dual abelian variety ![]() which is a quotient variety
of
which is a quotient variety
of ![]() .
.
theorem_type[remark][theorem][][remark][][] In this paper tex2html_wrap_inline$A_f$ always denotes an abelian subvariety of tex2html_wrap_inline$J_0(N)$. By abuse of notation, it is also common to denote by tex2html_wrap_inline$A_f$ the dual of the subvariety tex2html_wrap_inline$A_f$, which is a quotient of tex2html_wrap_inline$J_0(N)$ (see e.g. []).
6. ![]() -torsion submodules. If
-torsion submodules. If ![]() is a module over a commutative ring
is a module over a commutative ring ![]() and
and ![]() is an ideal of
is an ideal of ![]() , let
, let
be the
7. Hecke algebras. Let
![]() denote the space of cusp forms of weight
denote the space of cusp forms of weight ![]() for any
congruence subgroup
for any
congruence subgroup ![]() of
of
![]() . Let
. Let
be the Hecke algebra, where
8. Modular degree. If ![]() is an abelian subvariety of
is an abelian subvariety of ![]() , let
, let
be the induced polarization. The modular degree of
See [AS02] for why
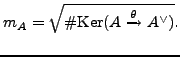 is an integer and for an algorithm to compute it.
is an integer and for an algorithm to compute it.
William Stein 2006-06-21