Theoretical Evidence for the Conjectures
The first piece of theoretical evidence for Conjecture 7.1.1 is Remark 3.0.2, according
to which any cohomology class
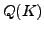 is visible in some abelian variety
is visible in some abelian variety 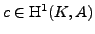 .
.
The next proposition gives evidence for elements of
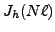 for an elliptic curve
for an elliptic curve 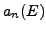 and elements
of order 2 or 3.
and elements
of order 2 or 3.
Proposition 7.2.1
Suppose 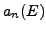 is an elliptic curve over
is an elliptic curve over
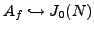 .
Then Conjecture 7.1.1 for
.
Then Conjecture 7.1.1 for 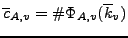 is true for all
elements of order
is true for all
elements of order 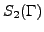 and
and 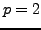 in
in
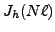 .
.
Proof.
We first show that there is an abelian
variety

of dimension
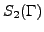
and an injective homomorphism
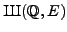
such that
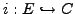
.
If
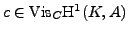
has order
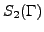
, this follows from
[
AS02, Prop. 2.4] or
[
Kle01],
and if
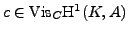
has order
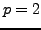
, this follows from
[
Maz99, Cor. pg. 224].
The quotient
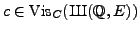
is an elliptic curve, so

is isogenous to a product
of two elliptic curves. Thus by
[
BCDT01],

is a quotient
of
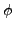
, for some
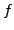
.
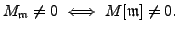
We also prove that Conjecture 7.1.1 is true with 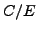 for all elements of
for all elements of
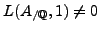 which split over abelian extensions.
which split over abelian extensions.
Proposition 7.2.2
Suppose
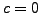 is a
is a 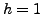 -modular abelian variety over
-modular abelian variety over
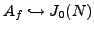 and
and
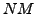 splits over an abelian extension of
splits over an abelian extension of
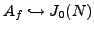 . Then
Conjecture 7.1.1 is true for
. Then
Conjecture 7.1.1 is true for 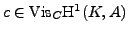 with
with 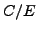 .
.
Proof.
Suppose
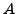
is an abelian extension such that
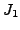
and let
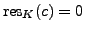
.
Then
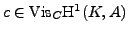
is visible in

(see Section
3.0.2). It remains to verify that

is modular. As discussed in [
Mil72, pg. 178], for any abelian variety
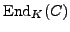
over
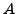
,
we have an isomorphism of Tate modules
and by Faltings's isogeny theorem [
Fal86], the Tate module determines an
abelian variety up to isogeny. Thus if
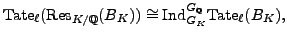
is an abelian variety attached to a
newform, then
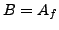
is isogenous to a product of
abelian varieties
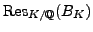
, where
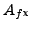
runs through
Dirichlet characters attached to the abelian extension
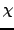
.
Since
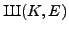
is isogenous to a product of abelian varieties of the form
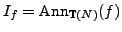
(for various
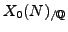
), it follows that the restriction of scalars

is modular.
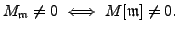
Remark 7.2.3
Suppose that
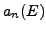
is an elliptic curve and
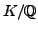
. Is there
an abelian extension
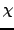
such that
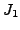
? The answer is ``yes'' if and only if there is a
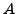
-rational point (with
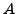
-abelian) on the locally trivial principal homogeneous space corresponding to
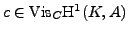
(this homogenous space is a genus one curve). Recently, M. Ciperiani and A. Wiles proved that any genus one curve over
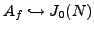
which
has local points everywhere and whose Jacobian is a semistable elliptic curve admits a point over a solvable
extension of
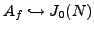
(see [
CW06]). Unfortunately, this paper does not answer our question about
the existence of abelian points.
Remark 7.2.4
As explained in [
Ste04], if
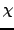
is an abelian extension of
prime degree then there is an exact sequence
where
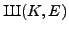
is an abelian variety with
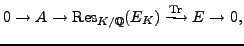
(here, the
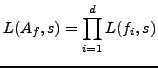
's
are the
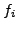
-conjugates of the twist of the newform
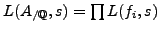
attached to
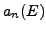
by the Dirichlet character associated to
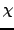
). Thus one could approach
the question in the previous remark by investigating whether or not
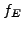
which one could do using modular symbols (see [
CFK06]).
The authors expect that
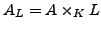
-functions of twists of degree larger than three are very
unlikely to vanish at
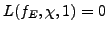
(see [
CFK06]), which suggests that in general,
the question might have a negative answer for cohomology classes of order larger than
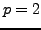
.
William Stein
2006-06-21
![]() is visible in some abelian variety
is visible in some abelian variety ![]() .
.
![]() for an elliptic curve
for an elliptic curve ![]() and elements
of order 2 or 3.
and elements
of order 2 or 3.
![]() for all elements of
for all elements of
![]() which split over abelian extensions.
which split over abelian extensions.
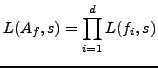 's
are the
's
are the