Results and a conjecture

We start by giving several results regarding the Manin constant for quotients of arbitrary dimension. The proofs of most of the theorems are given in Section 4.

Let $\Gamma$ be a subgroup of $\Gamma_0(N)$ that contains $\Gamma_1(N)$ . We have the following generalization of Edixhoven's Theorem 2.2.

Theorem 3.4   The Manin constant ${c_{\scriptscriptstyle{A}}}$ is an integer. (In the notation of Section 3.1 we even have that $\psi(H^0(A_{{\bf {Z}}},\Omega^1_{A/{\bf {Z}}})) \subseteq S_2({\bf {Z}})[I]$ .)

Proof. Let $J={\mathrm{Jac}}(X_\Gamma)$ and $J'=J_1(N)$ . Suppose $A$ is an optimal quotient of $J$ . We have natural maps $\H ^0(J'_{{\bf {Z}}}, \Omega^1_{J'/{\bf {Z}}}) \h... ...ga^1_{J'/{\bf {Q}}}) \stackrel{\cong }{\rightarrow } S_2(\Gamma_1(N);{\bf {Q}})$ ; from the proof of Lemma 6.1.6 of [CES03], the image of the composite is contained in  $S_2(\Gamma_1(N);{\bf {Z}})$ . The maps $J' \to J \to A$ induce a chain of inclusions

$$\H ^0(A_{{\bf {Z}}},\Omega^1_{A/{\bf... ...}}) \hookrightarrow S_2(\Gamma_1(N);{\bf {Z}}) \hookrightarrow {\bf {Z}}[[q]].$$

Combining this chain of inclusions with commutativity of the diagram

$$\xymatrix{ & {S_2(\Gamma_1(N))}\ar[dr]^{\text{$F$-exp}}\\ {S_2(\Gamma)} \ar[ur]^{f(q)\mapsto f(q)}\ar[rr]^{\text{$F$-exp}} & & {{\bf{C}}[[q]]}, }$$

where $F$ -exp is the Fourier expansion map, we see that the image of $\H ^0(A_{{\bf {Z}}},\Omega^1_{A/{\bf {Z}}})$ lies in $S_2({\bf {Z}})[I]$ , as claimed. $\qedsymbol$

For the rest of the paper, we take $\Gamma = \Gamma_0(N)$ . For each prime $\ell \mid N$ with ${\mathrm{ord}}_{\ell}(N)=1$ , let $W_\ell$ be the $\ell$ th Atkin-Lehner operator. Let $J=J_0(N)$ and $A = A_I = J/IJ$ be an optimal quotient of $J$ attached to a saturated ideal $I$ . If $\ell$ is a prime, then as usual, ${{\bf {Z}}_{(\ell)}}$ will denote the localization of ${\bf {Z}}$ at $\ell$ .

Theorem 3.5   Suppose that $\ell$ is an odd prime such that $\ell^2 \nmid N$ , and that if $\ell \mid N$ , then $A^{\vee}\subset J$ is stable under $W_{\ell}$ . Then $\ell \mid {c_{\scriptscriptstyle{A}}}$ if and only if $\ell \mid N$ and $S_2({{\bf {Z}}_{(\ell)}})[I]$ is not stable under the action of $W_\ell$ .

We will prove this theorem in Section 4.2.

Remark 3.6   The condition that $S_2({{\bf {Z}}_{(\ell)}})[I]$ is stable under $W_{\ell}$ can be verified using standard algorithms. Thus in light of Theorem 3.5, if $A$ is stable under all Atkin-Lehner operators and $N$ is square free, then one can compute the set of odd primes that divide $c_A$ . It would be interesting to refine the arguments of this paper to find an algorithm to compute $c_A$ exactly.

Let $J_{\rm old}$ denote the abelian subvariety of $J$ generated by the images of the degeneracy maps from levels that properly divide $N$ (see, e.g., [Maz78, §2(b)]) and let $J^{\rm new}$ denote the quotient of $J$ by  $J_{\rm old}$ . A new quotient is a quotient $J \to A$ that factors through the map $J \to J^{{\mathrm{new}}}$ . The following corollary generalizes Mazur's Theorem 2.3:

Corollary 3.7   If $A=A_f$ is an optimal newform quotient of $J_0(N)$ and $\ell \mid {c_{\scriptscriptstyle{A}}}$ is a prime, then $\ell = 2$ or $\ell^2 \mid N$ .

Proof. Since $f$ is a newform, $W_{\ell}$ acts as either $1$ or $-1$ on $A$ hence on $S_2({{\bf {Z}}_{(\ell)}})[I]$ . Thus $S_2({{\bf {Z}}_{(\ell)}})[I]$ is $W_{\ell}$ -stable. $\qedsymbol$

Corollary 3.8   If $A=J_0(N)_{{\mathrm{new}}}$ is the new subvariety of $J_0(N)$ and $\ell \mid {c_{\scriptscriptstyle{A}}}$ is a prime, then $\ell = 2$ or $\ell^2 \mid N$ . (In particular, if $N$ is prime then the Manin constant of $J_0(N)$ is a power of $2$ , since $A=J_0(N)[I]$ for $I=0$ .)

Proof. We have $W_{\ell} = -T_{\ell}$ on $A$ (e.g., see the end of [DI95, §6.3]). Also the new subspace $S_2({\bf {Z}})_{{\mathrm{new}}}$ of $S_2(\Gamma_0(N))$ is $T_{\ell}$ -stable. $\qedsymbol$

Remark 3.9   If $A=J_0(33)$ , then

$$W_{3} = \left(\begin{array}{rrr} 1&0... ...1}{3}&-\frac{4}{3}\\ \frac{1}{3}&-\frac{2}{3}&-\frac{1}{3} \end{array}\right)$$

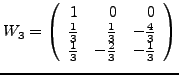
with respect to the basis

$$f_1 = q - q^{5} - 2q^{6} + 2q^{7} + \cdots,$$

$$f_2 = q^{2} - q^{4} - q^{5} - q^{6} + 2q^{7} + \cdots,$$

$$f_3 = q^{3} - 2q^{6} + \cdots$$

for $S_2({\bf {Z}})$ . Thus $W_3$ does not preserve $S_2({\bf {Z}}_{(3)})$ . In fact, the Manin constant of $J_0(33)$ is not $1$ in this case (see Section 3.4). Note that Theorem 3.5 implies that the only primes that can divide the Manin constant of any optimal quotient of tex2html_wrap_inline$J_0(33)$are tex2html_wrap_inline$2$ and tex2html_wrap_inline$3$.

The hypothesis of Theorem 3.5 sometimes holds for non-new $A$ . For example, take $J = J_0(33)$ and $\ell=3$ . Then $W_3$ acts as an endomorphism of $J$ , and a computation shows that the characteristic polynomial of $W_3$ on $S_2(33)_{{\mathrm{new}}}$ is $x-1$ and on $S_2(33)_{{\mathrm{old}}}$ is $(x-1)(x+1)$ , where $S_2(33)_{{\mathrm{old}}}$ is the old subspace of $S_2(33)$ . Consider the optimal elliptic curve quotient $A = J/(W_3+1)J$ , which is isogenous to $J_0(11)$ . Then $A$ is an optimal old quotient of $J$ , and $W_3$ acts as $-1$ on $A$ , so $W_3$ preserves the corresponding spaces of modular forms. Thus Theorem 3.5 implies that $3\nmid {c_{\scriptscriptstyle{A}}}$ .

The following theorem generalizes Raynaud's Theorem 2.4 (see also [GL01] for generalizations to ${\bf {Q}}$ -curves).

Theorem 3.10   If $f \in S_2(\Gamma_0(N))$ is a newform and $\ell$ is a prime such that $\ell^2 \nmid N$ , then ${\mathrm{ord}}_\ell({c_{\scriptscriptstyle{A_f}}}) \leq \dim A_f$ .

Note that in light of Theorem 3.5, this theorem gives new information only at $\ell = 2$ , when $2 \parallel N$ . We prove the theorem in Section 4.4

Let tex2html_wrap_inline$S_2(Z)[I]^&perp#perp;$ be the orthogonal complement of tex2html_wrap_inline$S_2(Z)[I]$ in tex2html_wrap_inline$S_2(Z)$ with respect to the Petersson inner product. theorem_type[defi][lem][][definition][][] [Congruence exponent and number] The congruence number tex2html_wrap_inline$r_A$ of tex2html_wrap_inline$A$is the order of the quotient group equation S_2(Z)/ (S_2(Z)[I] + S_2(Z)[I]^&perp#perp;). This definition of tex2html_wrap_inline$r_A$ agrees with Definition  when tex2html_wrap_inline$A$ is an elliptic curve (see [AU96, p. 276]).

Let $\pi$ denote the natural quotient map $J \rightarrow A$ . When we compose $\pi$ with its dual $A^{\vee}\rightarrow J^{\vee}$ (identifying $J^{\vee}$ with $J$ using the inverse of the principal polarization of $J$ ), we get an isogeny $\phi: A^{\vee}\rightarrow A$ . The modular exponent  ${m_{\scriptscriptstyle{A}}}$ of $A$ is the exponent of the group $\ker(\phi)$ . When $A$ is an elliptic curve, the modular exponent is just the modular degree of $A$ (see, e.g., [AU96, p. 278]).

Theorem 3.11   If $f \in S_2(\Gamma_0(N))$ is a newform and $\ell \mid {c_{\scriptscriptstyle{A_f}}}$ is a prime, then $\ell^2 \mid N$ or $\ell \mid {m_{\scriptscriptstyle{A}}}$ .

Again, in view of Corollary 3.7, this theorem gives new information only at $\ell = 2$ , when ${\mathrm{ord}}_2(N) \le 1$ . We prove the theorem in Section 4.3.

The theorems above suggest that the Manin constant is $1$ for quotients associated to newforms of square-free level. In the case when the level is not square free, computations of [FpS+01] involving Jacobians of genus $2$ curves that are quotients of  $J_0(N)^{\rm new}$ show that ${c_{\scriptscriptstyle{A}}}=1$ for $28$ two-dimensional newform quotients. These include quotients having the following non-square-free levels:

$$3^2\cdot 7,\quad 3^2\cdot 13, \quad 5^3,\quad 3^3\cdot 5,\quad 3\cdot 7^2, \quad 5^2\cdot 7, \quad 2^2\cdot 47, \quad 3^3\cdot 7.$$

The above observations suggest the following conjecture, which generalizes Conjecture 2.1:

Conjecture 3.12   If $f$ is a newform on $\Gamma_0(N)$ then ${c_{\scriptscriptstyle{A_f}}}=1$ .

It is plausible that ${c_{\scriptscriptstyle{A_f}}}=1$ for any newform on any congruence subgroup between $\Gamma_0(N)$ and $\Gamma_1(N)$ . However, we do not have enough data to justify making a conjecture in this context.