We will now prove the structure theorem for finitely generated abelian
groups, since it will be crucial for much of what we will do later.
Let
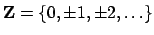 denote the ring of integers, and
for each positive integer
denote the ring of integers, and
for each positive integer 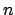 let
let
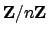 denote the ring of integers
modulo
denote the ring of integers
modulo 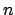 , which is a cyclic abelian group of order
, which is a cyclic abelian group of order 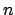 under
addition.
under
addition.
Definition 3.0.1 (Finitely Generated)
A group
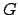
is
if there exists
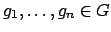
such that every element of
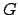
can be obtained from the
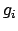
.
We will prove the theorem as follows. We first remark that any
subgroup of a finitely generated free abelian group is finitely
generated. Then we see that finitely generated abelian groups can be
presented as quotients of finite rank free abelian groups, and such a
presentation can be reinterpreted in terms of matrices over the
integers. Next we describe how to use row and column operations over
the integers to show that every matrix over the integers is equivalent
to one in a canonical diagonal form, called the Smith normal form. We
obtain a proof of the theorem by reinterpreting in
terms of groups.
Proposition 3.0.3
Suppose 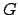 is a free abelian group of finite rank
is a free abelian group of finite rank 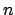 , and
, and 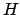 is a
subgroup of
is a
subgroup of 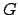 . Then
. Then 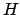 is a free abelian group generated by at
most
is a free abelian group generated by at
most 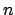 elements.
elements.
The key reason that this is true is that 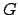 is a finitely generated
module over the principal ideal domain
is a finitely generated
module over the principal ideal domain
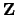 . We will give a complete
proof of a beautiful generalization of this result in the context of
Noetherian rings next time, but will not prove this proposition here.
. We will give a complete
proof of a beautiful generalization of this result in the context of
Noetherian rings next time, but will not prove this proposition here.
Corollary 3.0.4
Suppose 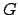 is a finitely generated abelian group. Then there are
finitely generated free abelian groups
is a finitely generated abelian group. Then there are
finitely generated free abelian groups 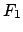 and
and 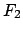 such that
such that
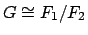 .
.
Proof.
Let
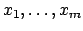
be generators for
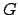
. Let
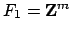
and let
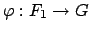
be the map that sends the
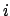
th generator
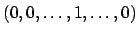
of
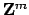
to
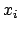
. Then
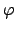
is
a surjective homomorphism, and by Proposition
3.0.4 the
kernel
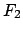
of
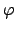
is a finitely generated free abelian group.
This proves the corollary.

Suppose 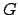 is a nonzero finitely generated abelian group. By the
corollary, there are free abelian groups
is a nonzero finitely generated abelian group. By the
corollary, there are free abelian groups 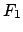 and
and 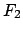 such that
such that
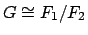 . Choosing a basis for
. Choosing a basis for 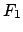 , we obtain an
isomorphism
, we obtain an
isomorphism
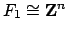 , for some positive integer
, for some positive integer 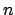 . By
Proposition 3.0.4,
. By
Proposition 3.0.4,
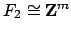 , for some integer
, for some integer 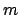 with
with
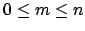 , and the inclusion map
, and the inclusion map
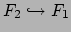 induces a map
induces a map
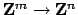 . This homomorphism is left
multiplication by the
. This homomorphism is left
multiplication by the 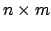 matrix
matrix  whose columns are the
images of the generators of
whose columns are the
images of the generators of 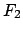 in
in
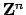 . The of
this homomorphism is the quotient of
. The of
this homomorphism is the quotient of
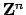 by the image of
by the image of  , and the
cokernel is isomorphic to
, and the
cokernel is isomorphic to 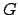 . By augmenting
. By augmenting  with zero columns on
the right we obtain a square
with zero columns on
the right we obtain a square 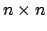 matrix
matrix  with the same
cokernel. The following proposition implies that we may choose bases
such that the matrix
with the same
cokernel. The following proposition implies that we may choose bases
such that the matrix  is diagonal, and then the structure of
the cokernel of
is diagonal, and then the structure of
the cokernel of  will be easy to understand.
will be easy to understand.
We will see in the proof of Theorem 3.0.3 that
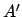 is uniquely determined by
is uniquely determined by  .
.
Proof.
The matrix
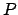
will be a product of matrices that define elementary
row operations and
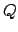
will be a product corresponding to elementary
column operations. The elementary operations are:
- Add an integer multiple of one row to another (or a multiple
of one column to another).
- Interchange two rows or two columns.
- Multiply a row by
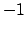 .
.
Each of these operations is given by left or right multiplying by an
invertible matrix
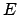
with integer entries, where
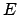
is the result of
applying the given operation to the identity matrix, and
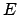
is
invertible because each operation can be reversed using another row or
column operation over the integers.
To see that the proposition must be true, assume 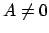 and perform
the following steps (compare [Art91, pg. 459]):
and perform
the following steps (compare [Art91, pg. 459]):
- By permuting rows and columns, move a nonzero entry of
 with
smallest absolute value to the upper left corner of
with
smallest absolute value to the upper left corner of  . Now attempt
to make all other entries in the first row and column 0 by adding
multiples of row or column 1 to other rows (see step 2 below). If an
operation produces a nonzero entry in the matrix with absolute value
smaller than
. Now attempt
to make all other entries in the first row and column 0 by adding
multiples of row or column 1 to other rows (see step 2 below). If an
operation produces a nonzero entry in the matrix with absolute value
smaller than 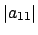 , start the process over by permuting rows and
columns to move that entry to the upper left corner of
, start the process over by permuting rows and
columns to move that entry to the upper left corner of  . Since the
integers
. Since the
integers 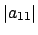 are a decreasing sequence of positive integers, we
will not have to move an entry to the upper left corner infinitely
often.
are a decreasing sequence of positive integers, we
will not have to move an entry to the upper left corner infinitely
often.
- Suppose
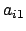 is a nonzero entry in the first column, with
is a nonzero entry in the first column, with
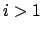 . Using the division algorithm, write
. Using the division algorithm, write
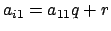 ,
with
,
with
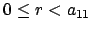 . Now add
. Now add 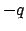 times the first row to the
times the first row to the
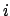 th row. If
th row. If 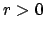 , then go to step 1 (so that an entry with
absolute value at most
, then go to step 1 (so that an entry with
absolute value at most 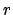 is the upper left corner). Since we will
only perform step 1 finitely many times, we may assume
is the upper left corner). Since we will
only perform step 1 finitely many times, we may assume 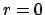 .
Repeating this procedure we set all entries in the first column
(except
.
Repeating this procedure we set all entries in the first column
(except 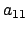 ) to 0. A similar process using column operations
sets each entry in the first row (except
) to 0. A similar process using column operations
sets each entry in the first row (except 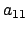 ) to 0.
) to 0.
- We may now assume that
 is the only nonzero entry in the
first row and column. If some entry
is the only nonzero entry in the
first row and column. If some entry 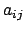 of
of  is not divisible
by
is not divisible
by 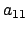 , add the column of
, add the column of  containing
containing 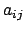 to the first
column, thus producing an entry in the first column that is nonzero.
When we perform step 2, the remainder
to the first
column, thus producing an entry in the first column that is nonzero.
When we perform step 2, the remainder 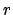 will be greater than 0.
Permuting rows and columns results in a smaller
will be greater than 0.
Permuting rows and columns results in a smaller 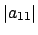 . Since
. Since
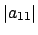 can only shrink finitely many times, eventually we will get
to a point where every
can only shrink finitely many times, eventually we will get
to a point where every 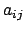 is divisible by
is divisible by 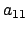 . If
. If 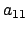 is negative, multiple the first row by
is negative, multiple the first row by 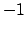 .
.
After performing the above operations, the first row and column
of

are zero except for
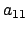
which is positive and divides
all other entries of

. We repeat the above steps for the
matrix

obtained from

by deleting the first row and column.
The upper left entry of the resulting matrix will be divisible by
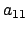
, since every entry of

is. Repeating the argument
inductively proves the proposition.

Example 3.0.6
The matrix
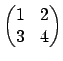
is equivalent
to
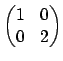
and the matrix
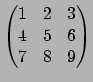
is equivalent to

Note that the determinants match, up to sign.
Proof.
[Theorem
3.0.3]
Suppose
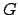
is a finitely generated abelian group, which we may assume
is nonzero. As in the paragraph before Proposition
3.0.6,
we use Corollary
3.0.5 to write
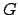
as a the cokernel
of an
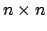
integer matrix

. By Proposition
3.0.6
there are isomorphisms
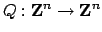
and
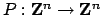
such that
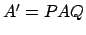
is a diagonal matrix with entries
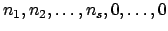
, where
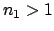
and
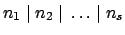
. Then
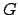
is isomorphic to the cokernel of the diagonal matrix
, so
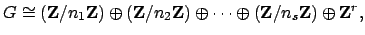 |
(3.1) |
as claimed. The
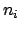
are determined by
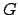
, because
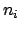
is the
smallest positive integer
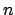
such that
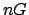
requires at most
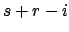
generators (we see from the representation (
3.0.1) of
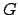
as
a product that
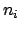
has this property and that no smaller positive
integer does).

William Stein
2004-05-06
![]() denote the ring of integers, and
for each positive integer
denote the ring of integers, and
for each positive integer ![]() let
let
![]() denote the ring of integers
modulo
denote the ring of integers
modulo ![]() , which is a cyclic abelian group of order
, which is a cyclic abelian group of order ![]() under
addition.
under
addition.
![]() is a nonzero finitely generated abelian group. By the
corollary, there are free abelian groups
is a nonzero finitely generated abelian group. By the
corollary, there are free abelian groups ![]() and
and ![]() such that
such that
![]() . Choosing a basis for
. Choosing a basis for ![]() , we obtain an
isomorphism
, we obtain an
isomorphism
![]() , for some positive integer
, for some positive integer ![]() . By
Proposition 3.0.4,
. By
Proposition 3.0.4,
![]() , for some integer
, for some integer ![]() with
with
![]() , and the inclusion map
, and the inclusion map
![]() induces a map
induces a map
![]() . This homomorphism is left
multiplication by the
. This homomorphism is left
multiplication by the ![]() matrix
matrix ![]() whose columns are the
images of the generators of
whose columns are the
images of the generators of ![]() in
in
![]() . The of
this homomorphism is the quotient of
. The of
this homomorphism is the quotient of
![]() by the image of
by the image of ![]() , and the
cokernel is isomorphic to
, and the
cokernel is isomorphic to ![]() . By augmenting
. By augmenting ![]() with zero columns on
the right we obtain a square
with zero columns on
the right we obtain a square ![]() matrix
matrix ![]() with the same
cokernel. The following proposition implies that we may choose bases
such that the matrix
with the same
cokernel. The following proposition implies that we may choose bases
such that the matrix ![]() is diagonal, and then the structure of
the cokernel of
is diagonal, and then the structure of
the cokernel of ![]() will be easy to understand.
will be easy to understand.
![]() and perform
the following steps (compare [Art91, pg. 459]):
and perform
the following steps (compare [Art91, pg. 459]):
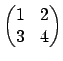 is equivalent
to
is equivalent
to
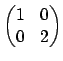 and the matrix
and the matrix
 is equivalent to
is equivalent to
 Note that the determinants match, up to sign.
Note that the determinants match, up to sign.![]()