We need only a special case of the tensor product construction.
Let  and
and  be commutative rings containing a field
be commutative rings containing a field  and suppose that
and suppose that  is of finite dimension
is of finite dimension 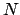 over
over  , say, with basis
Then
, say, with basis
Then  is determined up to isomorphism as a ring over
is determined up to isomorphism as a ring over  by the multiplication table
by the multiplication table
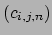 defined by
We define a new ring
defined by
We define a new ring 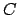 containing
containing  whose elements are
the set of all expressions
where the
whose elements are
the set of all expressions
where the
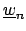 have the same multiplication rule
as the
have the same multiplication rule
as the 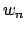 .
.
There are injective ring homomorphisms

(note that $
w_1=1$)
and
Moreover 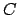 is defined, up to isomorphism, by
is defined, up to isomorphism, by  and
and  and is
independent of the particular choice of basis
and is
independent of the particular choice of basis 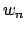 of
of  (i.e., a
change of basis of
(i.e., a
change of basis of  induces a canonical isomorphism of the
induces a canonical isomorphism of the 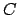 defined by the first basis to the
defined by the first basis to the 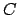 defined by the second basis).
We write
since
defined by the second basis).
We write
since 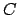 is, in fact, a special case of the ring tensor product.
is, in fact, a special case of the ring tensor product.
Let us now suppose, further, that  is a topological ring, i.e., has
a topology with respect to which addition and multiplication are
continuous. Then the map
is a topological ring, i.e., has
a topology with respect to which addition and multiplication are
continuous. Then the map
defines a bijection between 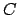 and the product of
and the product of 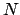 copies of
copies of  (considered as sets). We give
(considered as sets). We give 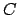 the product topology. It is readily
verified that this topology is independent of the choice of basis
the product topology. It is readily
verified that this topology is independent of the choice of basis
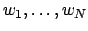 and that multiplication and addition on
and that multiplication and addition on  are
continuous, so
are
continuous, so  is a topological ring. We call this topology
on
is a topological ring. We call this topology
on 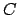 the .
the .
Now drop our assumption that  and
and  have a topology, but suppose
that
have a topology, but suppose
that  and
and  are not merely rings but fields. Recall that a
finite extension
are not merely rings but fields. Recall that a
finite extension 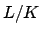 of fields is if the number of
embeddings
of fields is if the number of
embeddings
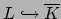 that fix
that fix  equals the degree of
equals the degree of 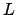 over
over  , where
, where
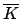 is an algebraic closure of
is an algebraic closure of  . The primitive
element theorem from Galois theory asserts that any such extension is
generated by a single element, i.e.,
. The primitive
element theorem from Galois theory asserts that any such extension is
generated by a single element, i.e., 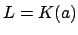 for some
for some 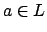 .
.
Lemma 18.2.1
Let  and
and  be fields containing the field
be fields containing the field  and suppose
that
and suppose
that  is a separable extension of finite degree
is a separable extension of finite degree ![$ N=[B:K]$](img2121.png) . Then
. Then
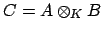 is the direct sum of a finite number of fields
is the direct sum of a finite number of fields
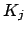 , each containing an isomorphic image of
, each containing an isomorphic image of  and an isomorphic
image of
and an isomorphic
image of  .
.
Proof.
By the primitive element theorem, we have
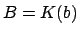
, where
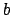
is a
root of some separable irreducible polynomial
![$ f(x)\in K[x]$](img2125.png)
of
degree
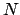
. Then
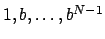
is a basis
for

over

, so
where
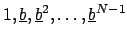
are
linearly independent over

and
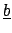
satisfies
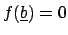
.
Although the polynomial 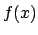 is irreducible as an element
of
is irreducible as an element
of ![$ K[x]$](img304.png) , it need not be irreducible in
, it need not be irreducible in ![$ A[x]$](img2131.png) . Since
. Since  is a field, we have a factorization
is a field, we have a factorization
where
![$ g_j(x)\in A[x]$](img2133.png)
is irreducible. The
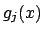
are
distinct because
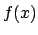
is separable (i.e., has distinct
roots in any algebraic closure).
For each 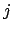 , let
, let
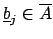 be a root of
be a root of 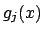 , where
, where
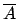 is a fixed
algebraic closure of the field
is a fixed
algebraic closure of the field  . Let
. Let
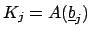 .
Then the map
.
Then the map
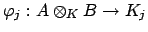 |
(18.1) |
given by sending any polynomial
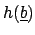
in
(where
![$ h\in A[x]$](img2140.png)
)
to
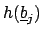
is a ring homomorphism, because the image
of
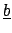
satisfies the polynomial
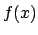
, and
![$ A\otimes _K B\cong A[x]/(f(x))$](img2142.png)
.
By the Chinese Remainder Theorem, the maps from (18.2.1)
combine to define a ring isomorphism
Each 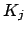 is of the form
is of the form
![$ A[x]/(g_j(x))$](img2144.png) , so contains an isomorphic
image of
, so contains an isomorphic
image of  . It thus remains to show that the ring
homomorphisms
. It thus remains to show that the ring
homomorphisms
are injections. Since

and
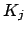
are both fields,
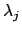
is either the
0 map or injective. However,
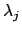
is
not the
0 map since
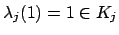
.

Example 18.2.2
If

and

are finite extensions of
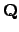
, then
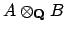
is an algebra of degree
![$ [A:\mathbf{Q}]\cdot [B:\mathbf{Q}]$](img2149.png)
. For example, suppose

is generated by a root of
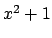
and

is generated by a root
of
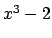
. We can view
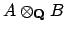
as either
![$ A[x]/(x^3-2)$](img2151.png)
or
![$ B[x]/(x^2+1)$](img2152.png)
. The polynomial
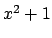
is irreducible over
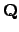
,
and if it factored over the cubic field

, then there would be a
root of
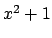
in

, i.e., the quadratic field
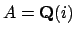
would be
a subfield of the cubic field
![$ B=\mathbf{Q}(\sqrt[3]{2})$](img2154.png)
, which is
impossible. Thus
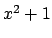
is irreducible over

, so
![$ A\otimes _\mathbf{Q}B
= A.B = \mathbf{Q}(i,\sqrt[3]{2})$](img2155.png)
is a degree
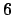
extension of
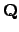
.
Notice that
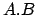
contains a copy

and a copy of

. By the
primitive element theorem the composite field
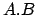
can be generated
by the root of a single polynomial. For example, the minimal
polynomial of
![$ i+\sqrt[3]{2}$](img2157.png)
is
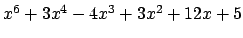
, hence
![$ \mathbf{Q}(i+\sqrt[3]{2})=A.B$](img2159.png)
.
Example 18.2.3
The case
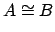
is even more exciting. For example, suppose
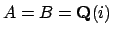
. Using the Chinese Remainder Theorem we have that
since
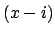
and
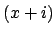
are coprime. The last isomorphism
sends
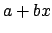
, with
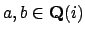
, to
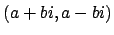
.
Since
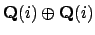
has zero divisors, the tensor
product
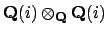
must also have zero divisors.
For example,
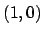
and
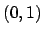
is a zero divisor pair
on the right hand side, and we can trace back to the elements
of the tensor product that they define. First, by solving
the system
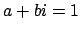
and
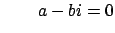
we see that
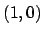
corresponds to
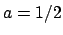
and
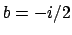
, i.e., to the element
This element in turn
corresponds to
Similarly the other element
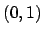
corresponds to
As a double check, observe that
Clearing the denominator of
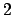
and writing
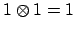
, we have
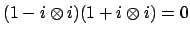
, so
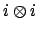
is a root of the
polynomimal
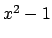
, and
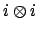
is not
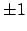
, so
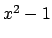
has
more than
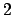
roots.
In general, to understand
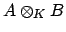 explicitly
is the same as factoring either the defining polynomial of
explicitly
is the same as factoring either the defining polynomial of  over the field
over the field  , or factoring the defining polynomial of
, or factoring the defining polynomial of  over
over  .
.
Proof.
We show that both sides of (
18.2.2) are the characteristic
polynomial
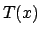
of the image of

in
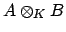
over

.
That
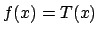
follows at once by computing the characteristic
polynomial in terms of a basis
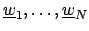
of
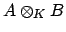
, where
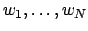
is a basis for

over

(this is
because the matrix of left multiplication by
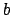
on
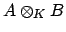
is exactly the same as the matrix of left multiplication on

, so
the characteristic polynomial doesn't change). To see that
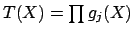
, compute the action of the image of

in
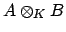
with respect to a basis of
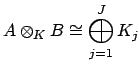 |
(18.3) |
composed of basis of the individual extensions
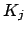
of

. The
resulting matrix will be a block direct sum of submatrices, each of
whose characteristic polynomials is one of the
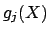
. Taking
the product gives the claimed identity (
18.2.2).

Corollary 18.2.5
For 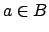 we have
and
we have
and
Proof.
This follows from Corollary
18.2.4. First, the norm is
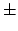
the constant term of the characteristic polynomial, and the constant
term of the product of polynomials is the product of the constant
terms (and one sees that the sign matches up correctly). Second,
the trace is minus the second coefficient of the characteristic
polynomial, and second coefficients add when one multiplies
polynomials:
One could also see both the statements by considering a matrix of
left multiplication by

first with respect to the basis of
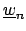
and second with respect to the basis coming from the left
side of (
18.2.3).

William Stein
2004-05-06
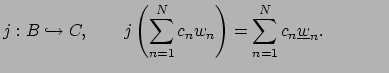
![]() is a topological ring, i.e., has
a topology with respect to which addition and multiplication are
continuous. Then the map
is a topological ring, i.e., has
a topology with respect to which addition and multiplication are
continuous. Then the map
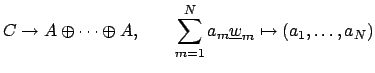
![]() and
and ![]() have a topology, but suppose
that
have a topology, but suppose
that ![]() and
and ![]() are not merely rings but fields. Recall that a
finite extension
are not merely rings but fields. Recall that a
finite extension ![]() of fields is if the number of
embeddings
of fields is if the number of
embeddings
![]() that fix
that fix ![]() equals the degree of
equals the degree of ![]() over
over ![]() , where
, where
![]() is an algebraic closure of
is an algebraic closure of ![]() . The primitive
element theorem from Galois theory asserts that any such extension is
generated by a single element, i.e.,
. The primitive
element theorem from Galois theory asserts that any such extension is
generated by a single element, i.e., ![]() for some
for some ![]() .
.
![]() is irreducible as an element
of
is irreducible as an element
of ![]() , it need not be irreducible in
, it need not be irreducible in ![]() . Since
. Since ![]() is a field, we have a factorization
is a field, we have a factorization
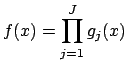
![]() , let
, let
![]() be a root of
be a root of ![]() , where
, where
![]() is a fixed
algebraic closure of the field
is a fixed
algebraic closure of the field ![]() . Let
. Let
![]() .
Then the map
.
Then the map
![$\displaystyle A\otimes _K B \cong A[x]/(f(x)) \cong \bigoplus_{j=1}^J A[x]/(g_j(x))
\cong \bigoplus_{j=1}^J K_j.
$](img2143.png)
![]() is of the form
is of the form
![]() , so contains an isomorphic
image of
, so contains an isomorphic
image of ![]() . It thus remains to show that the ring
homomorphisms
. It thus remains to show that the ring
homomorphisms
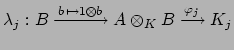
![$\displaystyle \frac{1}{2}- \frac{i}{2} x\in \mathbf{Q}(i)[x]/(x^2+1).$](img2174.png)
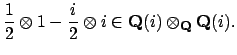
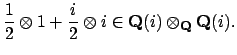
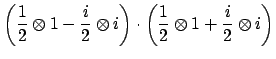
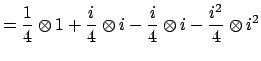
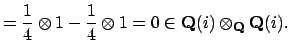
![]() explicitly
is the same as factoring either the defining polynomial of
explicitly
is the same as factoring either the defining polynomial of ![]() over the field
over the field ![]() , or factoring the defining polynomial of
, or factoring the defining polynomial of ![]() over
over ![]() .
.![]()