Next: Types of Valuations Up: Valuations Previous: Valuations Contents Index
The is the valuation for which
![]() for all
for all ![]() . We will often tacitly
exclude the trivial valuation from consideration.
. We will often tacitly
exclude the trivial valuation from consideration.
From (2) we have
If
![]() is a valuation and
is a valuation and ![]() is the constant from Axiom
(3), then there is a
is the constant from Axiom
(3), then there is a ![]() such that
such that ![]() (i.e.,
(i.e.,
![]() ). Then we can take
). Then we can take ![]() as constant for the
equivalent valuation
as constant for the
equivalent valuation
![]() . Thus every valuation is
equivalent to a valuation with
. Thus every valuation is
equivalent to a valuation with ![]() . Note that if
. Note that if ![]() , e.g.,
if
, e.g.,
if
![]() is the trivial valuation, then we could
simply take
is the trivial valuation, then we could
simply take ![]() in Axiom (3).
in Axiom (3).
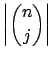 and using
the binomial expansion, we have for any
and using
the binomial expansion, we have for any 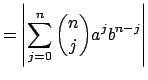 |
||
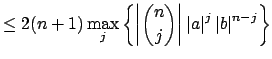 |
||
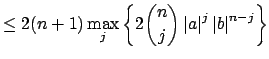 |
||
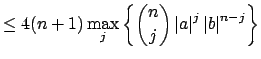 |
||
William Stein 2004-05-06