A  is a finite algebraic extension
of the rational numbers
is a finite algebraic extension
of the rational numbers
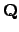 . Every such extension can be
represented as all polynomials in an algebraic number
. Every such extension can be
represented as all polynomials in an algebraic number 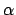 :
Here
:
Here 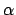 is a root of a polynomial with coefficients in
is a root of a polynomial with coefficients in
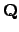 .
Note that
tex2html_wrap_inline$Q(&alpha#alpha;)$ is non-canonically isomorphic to tex2html_wrap_inline$Q[x]/(f)$, where tex2html_wrap_inline$f$is the minimal polynomial of tex2html_wrap_inline$&alpha#alpha;$. The isomorphism is induced by
the homomorphism tex2html_wrap_inline$Q[x]&rarr#to;Q(&alpha#alpha;)$ that sends tex2html_wrap_inline$x$ to tex2html_wrap_inline$&alpha#alpha;$,
which has kernel tex2html_wrap_inline$(f)$. It is not canonical, since tex2html_wrap_inline$Q(&alpha#alpha;)$ could
have nontrivial automorphisms. For example, if tex2html_wrap_inline$&alpha#alpha;=2$, then
tex2html_wrap_inline$Q(2)$ is isomorphic as a field to tex2html_wrap_inline$Q(-2)$ via
tex2html_wrap_inline$2&map#mapsto;-2$. There are two isomorphisms
tex2html_wrap_inline$Q[x]/(x^2-2)&rarr#to;Q(2)$.
.
Note that
tex2html_wrap_inline$Q(&alpha#alpha;)$ is non-canonically isomorphic to tex2html_wrap_inline$Q[x]/(f)$, where tex2html_wrap_inline$f$is the minimal polynomial of tex2html_wrap_inline$&alpha#alpha;$. The isomorphism is induced by
the homomorphism tex2html_wrap_inline$Q[x]&rarr#to;Q(&alpha#alpha;)$ that sends tex2html_wrap_inline$x$ to tex2html_wrap_inline$&alpha#alpha;$,
which has kernel tex2html_wrap_inline$(f)$. It is not canonical, since tex2html_wrap_inline$Q(&alpha#alpha;)$ could
have nontrivial automorphisms. For example, if tex2html_wrap_inline$&alpha#alpha;=2$, then
tex2html_wrap_inline$Q(2)$ is isomorphic as a field to tex2html_wrap_inline$Q(-2)$ via
tex2html_wrap_inline$2&map#mapsto;-2$. There are two isomorphisms
tex2html_wrap_inline$Q[x]/(x^2-2)&rarr#to;Q(2)$.
involves using techniques from (mostly
commutative) algebra and finite group theory to gain a deeper
understanding of number fields. The main objects that we study in
algebraic number theory are number fields, rings of integers of number
fields, unit groups, ideal class groups,norms, traces, discriminants,
prime ideals, Hilbert and other class fields and associated
reciprocity laws, zeta and 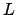 -functions, and algorithms for computing
each of the above.
-functions, and algorithms for computing
each of the above.
Subsections
William Stein
2004-05-06
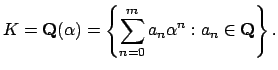
![]() -functions, and algorithms for computing
each of the above.
-functions, and algorithms for computing
each of the above.