Next: A Method for Factoring Up: Factoring Primes Previous: Factoring Primes Contents Index
![$\displaystyle \xymatrix{
{(??) }\ar@{^(->}[r]\ar[d] &{\Spec (\O _K)}\ar[d] \\...
...pec(\Z[x]/g(x))\\
{\Spec (\mathbf{F}_p) }\ar@{^(->}[r]&{\Spec (\mathbf{Z})}
}$](img505.png)
The cover
![]() is easy to understand
because it is defined by the single equation
is easy to understand
because it is defined by the single equation ![]() . To give a
maximal ideal
. To give a
maximal ideal
![]() of
of
![]() such that
such that
![]() is the
same as giving a homomorphism
is the
same as giving a homomorphism
![]() (up to
automorphisms of the image), which is in turn the same as giving a
root of
(up to
automorphisms of the image), which is in turn the same as giving a
root of ![]() in
in
![]() (up to automorphism), which is the same
as giving an irreducible factor of the reduction of
(up to automorphism), which is the same
as giving an irreducible factor of the reduction of ![]() modulo
modulo ![]() .
.
As suggested in the proof of the lemma, we find all homomorphisms
![]() by finding all homomorphism
by finding all homomorphism
![]() . In
terms of ideals, if
. In
terms of ideals, if
![]() is a maximal ideal of
is a maximal ideal of
![]() ,
then the ideal
,
then the ideal
![]() of
of ![]() is also maximal, since
is also maximal, since
We formalize the above discussion in the following theorem:
![$\displaystyle \overline{f} = \prod_{i=1}^t \overline{f}_i^{e_i} \in \mathbf{F}_p[x]
$](img528.png)
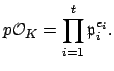
We return to the example from above, in which
![]() , where
, where ![]() is
a root of
is
a root of
![]() . According to , the maximal
order
. According to , the maximal
order ![]() has discriminant
has discriminant ![]() :
:
> Discriminant(MaximalOrder(K)); 2945785The order
> Discriminant(x^5 + 7*x^4 + 3*x^2 - x + 1); 2945785We have
If we replace ![]() by
by ![]() , then the index of
, then the index of
![]() in
in ![]() will be a power of
will be a power of ![]() , which is coprime to
, which is coprime to ![]() ,
so the above method will still work.
,
so the above method will still work.
> f:=MinimalPolynomial(7*a);
> f;
x^5 + 49*x^4 + 1029*x^2 - 2401*x + 16807
> Discriminant(f);
235050861175510968365785
> Discriminant(f)/Discriminant(MaximalOrder(K));
79792266297612001 // coprime to 5
> S<t> := PolynomialRing(GF(5));
> Factorization(S!f);
[
<t + 1, 2>,
<t + 4, 1>,
<t^2 + 3*t + 3, 1>
]
Thus
> f:=MinimalPolynomial(5*a);
> f;
x^5 + 35*x^4 + 375*x^2 - 625*x + 3125
> Discriminant(f) / Discriminant(MaximalOrder(K));
95367431640625 // divisible by 5
> Factorization(S!f);
[
<t, 5>
]
William Stein 2004-05-06