Next: and Number Fields Up: Using Previous: Using Contents Index
> A := Matrix(2,2,[1,2,3,4]); > A; [1 2] [3 4] > SmithForm(A); [1 0] [0 2] [ 1 0] [-1 1] [-1 2] [ 1 -1]As you can see, computed the Smith form, which is
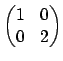 . What are the other two matrices
it output? To see what any command does, type
the command by itself with no arguments followed by a
semicolon.
. What are the other two matrices
it output? To see what any command does, type
the command by itself with no arguments followed by a
semicolon.
> SmithForm;
Intrinsic 'SmithForm'
Signatures:
(<Mtrx> X) -> Mtrx, AlgMatElt, AlgMatElt
[
k: RngIntElt,
NormType: MonStgElt,
Partial: BoolElt,
RightInverse: BoolElt
]
The smith form S of X, together with unimodular matrices
P and Q such that P * X * Q = S.
As you can see, SmithForm returns three arguments, a matrix and
matrices > S, P, Q := SmithForm(A); > S; [1 0] [0 2] > P; [ 1 0] [-1 1] > Q; [-1 2] [ 1 -1] > P*A*Q; [1 0] [0 2]Next, let's test the limits. We make a
> A := Matrix(10,10,[Random(100) : i in [1..100]]); > time B := SmithForm(A); Time: 0.000Let's print the first row of
> A[1]; ( 4 48 84 3 58 61 53 26 9 5) > B[1]; (1 0 0 0 0 0 0 0 0 0) > B[10]; (0 0 0 0 0 0 0 0 0 51805501538039733) > [B[i,i] : i in [1..10]]; [ 1, 1, 1, 1, 1, 1, 1, 1, 1, 51805501538039733 ]Let's see how big we have to make
> n := 50; A := Matrix(n,n,[Random(100) : i in [1..n^2]]); > time B := SmithForm(A); Time: 0.050 > n := 100; A := Matrix(n,n,[Random(100) : i in [1..n^2]]); > time B := SmithForm(A); Time: 0.800 > n := 150; A := Matrix(n,n,[Random(100) : i in [1..n^2]]); > time B := SmithForm(A); Time: 4.900 > n := 200; A := Matrix(n,n,[Random(100) : i in [1..n^2]]); > time B := SmithForm(A); Time: 19.160
can also work with finitely generated abelian groups.
> G := AbelianGroup([3,5,18]);
> G;
Abelian Group isomorphic to Z/3 + Z/90
Defined on 3 generators
Relations:
3*G.1 = 0
5*G.2 = 0
18*G.3 = 0
> #G;
270
> H := sub<G | [G.1+G.2]>;
> #H;
15
> G/H;
Abelian Group isomorphic to Z/18
William Stein 2004-05-06