Before discussing norms and traces we introduce some notation for
field extensions. If
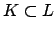 are number fields, we let
are number fields, we let ![$ [L:K]$](img281.png) denote the dimension of
denote the dimension of 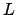 viewed as a
viewed as a  -vector space. If
-vector space. If  is a
number field and
is a
number field and
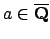 , let
, let 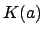 be the number field
generated by
be the number field
generated by  , which is the smallest number field that
contains
, which is the smallest number field that
contains  . If
. If
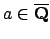 then
then  has a minimal polynomial
has a minimal polynomial
![$ f(x)\in\mathbf{Q}[x]$](img271.png) , and the of
, and the of  are the roots
of
are the roots
of 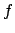 . For example the element
. For example the element 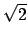 has minimal polynomial
has minimal polynomial
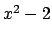 and the Galois conjugates of
and the Galois conjugates of 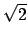 are
are
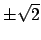 .
.
Suppose
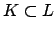 is an inclusion of number fields and let
is an inclusion of number fields and let 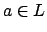 . Then left multiplication by
. Then left multiplication by  defines a
defines a  -linear
transformation
-linear
transformation
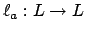 . (The transformation
. (The transformation 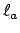 is
is
 -linear because
-linear because 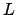 is commutative.)
is commutative.)
Definition 5.2.1 (Norm and Trace)
The
and
of

from
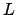
to

are
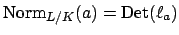
and
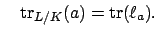
It is standard from linear algebra that
determinants are multiplicative
and traces are additive, so for 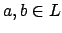 we have
and
we have
and
Note that if
![$ f\in\mathbf{Q}[x]$](img205.png) is the characteristic polynomial of
is the characteristic polynomial of  ,
then the constant term of
,
then the constant term of 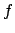 is
is
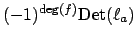 , and the
coefficient of
, and the
coefficient of
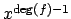 is
is
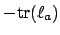 .
.
Proof.
We prove the proposition by computing the characteristic
polynomial
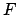
of

. Let
![$ f\in K[x]$](img303.png)
be the minimal polynomial
of

over

, and note that
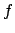
has distinct roots (since it is the
polynomial in
![$ K[x]$](img304.png)
of least degree that is satisfied by

).
Since
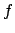
is irreducible,
![$ [K(a):K]=\deg(f)$](img305.png)
, and

satisfies a
polynomial if and only if
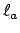
does, the characteristic polynomial
of
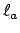
acting on
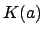
is
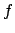
. Let
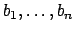
be a basis
for
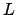
over
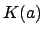
and note that
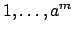
is a basis for
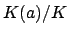
, where
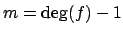
. Then
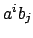
is a basis for
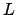
over

, and left multiplication by

acts the same way on the span of
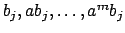
as on the span of
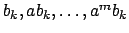
, for any pair
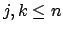
. Thus the matrix of
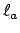
on
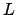
is a block direct sum of copies of the matrix of
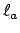
acting
on
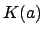
, so the characteristic polynomial of
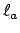
on
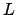
is
![$ f^{[L:K(a)]}$](img314.png)
. The proposition follows because the roots of
![$ f^{[L:K(a)]}$](img314.png)
are exactly the images
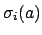
, with multiplicity
![$ [L:K(a)]$](img316.png)
(since each embedding of
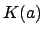
into
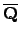
extends in
exactly
![$ [L:K(a)]$](img316.png)
ways to
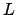
by Exercise
9).

The following corollary asserts that the norm and trace behave well in
towers.
Corollary 5.2.3
Suppose
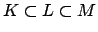 is a tower of number fields, and
let
is a tower of number fields, and
let 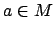 . Then
. Then

and
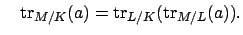
Proof.
For the first equation, both sides are the product of
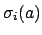
,
where
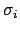
runs through the embeddings of
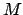
into

. To see
this, suppose
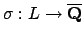
fixes

. If
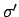
is an
extension of
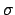
to
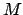
, and
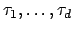
are the
embeddings of
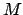
into
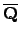
that fix
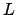
, then
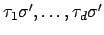
are exactly the extensions of
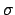
to
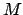
. For the second statement, both sides are the sum of
the
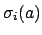
.

The norm and trace down to
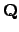 of an algebraic integer
of an algebraic integer  is an
element of
is an
element of
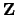 , because the minimal polynomial of
, because the minimal polynomial of  has integer
coefficients, and the characteristic polynomial of
has integer
coefficients, and the characteristic polynomial of  is a power of the
minimal polynomial, as we saw in the proof of
Proposition 5.2.2.
is a power of the
minimal polynomial, as we saw in the proof of
Proposition 5.2.2.
Proposition 5.2.4
Let  be a number field. The ring of integers
be a number field. The ring of integers  is a lattice
in
is a lattice
in  , i.e.,
, i.e.,
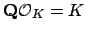 and
and  is an abelian group of rank
is an abelian group of rank
![$ [K:\mathbf{Q}]$](img327.png) .
.
Proof.
We saw in Lemma
5.1.8 that
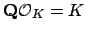
. Thus there exists a
basis
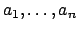
for

, where each
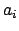
is in

.
Suppose that as
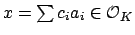
varies over all elements of

the denominators of the coefficients
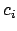
are arbitrarily
large. Then subtracting off integer multiples of the
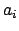
, we see
that as
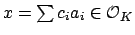
varies over elements of

with
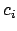
between
0 and
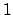
, the denominators of the
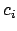
are also
arbitrarily large. This implies that there are infinitely many elements
of

in the bounded subset
Thus for any
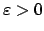
, there are elements
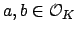
such that the
coefficients of
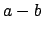
are all less than
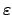
(otherwise the elements
of

would all be a ``distance'' of least
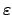
from each other, so only finitely
many of them would fit in
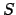
).
As mentioned above, the norms of elements of  are integers.
Since the norm of an element is the determinant of left multiplication
by that element, the norm is a homogenous polynomial of degree
are integers.
Since the norm of an element is the determinant of left multiplication
by that element, the norm is a homogenous polynomial of degree 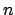 in
the indeterminate coefficients
in
the indeterminate coefficients 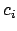 . If the
. If the 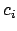 get arbitrarily
small for elements of
get arbitrarily
small for elements of  , then the values of the norm polynomial
get arbitrarily small, which would imply that there are elements of
, then the values of the norm polynomial
get arbitrarily small, which would imply that there are elements of
 with positive norm too small to be in
with positive norm too small to be in
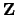 , a contradiction.
So the set
, a contradiction.
So the set 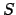 contains only finitely many elements of
contains only finitely many elements of  . Thus
the denominators of the
. Thus
the denominators of the 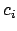 are bounded, so for some
are bounded, so for some 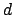 , we have
that
, we have
that  has finite index in
has finite index in
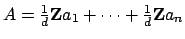 . Since
. Since  is isomorphic to
is isomorphic to
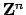 , it follows
from the structure theorem for finitely generated abelian groups that
, it follows
from the structure theorem for finitely generated abelian groups that
 is isomorphic as a
is isomorphic as a
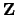 -module to
-module to
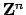 , as claimed.
, as claimed.

Proof.
By Proposition
5.2.4, the ring

is
finitely generated as a module over
, so it is certainly
finitely generated as a ring over
. By the Hilbert
Basis Theorem,

is Noetherian.

William Stein
2004-05-06
![]() is an inclusion of number fields and let
is an inclusion of number fields and let ![]() . Then left multiplication by
. Then left multiplication by ![]() defines a
defines a ![]() -linear
transformation
-linear
transformation
![]() . (The transformation
. (The transformation ![]() is
is
![]() -linear because
-linear because ![]() is commutative.)
is commutative.)
![]() is the characteristic polynomial of
is the characteristic polynomial of ![]() ,
then the constant term of
,
then the constant term of ![]() is
is
![]() , and the
coefficient of
, and the
coefficient of
![]() is
is
![]() .
.
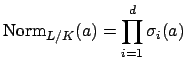 and
and 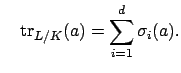
![]() of an algebraic integer
of an algebraic integer ![]() is an
element of
is an
element of
![]() , because the minimal polynomial of
, because the minimal polynomial of ![]() has integer
coefficients, and the characteristic polynomial of
has integer
coefficients, and the characteristic polynomial of ![]() is a power of the
minimal polynomial, as we saw in the proof of
Proposition 5.2.2.
is a power of the
minimal polynomial, as we saw in the proof of
Proposition 5.2.2.
![]() are integers.
Since the norm of an element is the determinant of left multiplication
by that element, the norm is a homogenous polynomial of degree
are integers.
Since the norm of an element is the determinant of left multiplication
by that element, the norm is a homogenous polynomial of degree ![]() in
the indeterminate coefficients
in
the indeterminate coefficients ![]() . If the
. If the ![]() get arbitrarily
small for elements of
get arbitrarily
small for elements of ![]() , then the values of the norm polynomial
get arbitrarily small, which would imply that there are elements of
, then the values of the norm polynomial
get arbitrarily small, which would imply that there are elements of
![]() with positive norm too small to be in
with positive norm too small to be in
![]() , a contradiction.
So the set
, a contradiction.
So the set ![]() contains only finitely many elements of
contains only finitely many elements of ![]() . Thus
the denominators of the
. Thus
the denominators of the ![]() are bounded, so for some
are bounded, so for some ![]() , we have
that
, we have
that ![]() has finite index in
has finite index in
![]() . Since
. Since ![]() is isomorphic to
is isomorphic to
![]() , it follows
from the structure theorem for finitely generated abelian groups that
, it follows
from the structure theorem for finitely generated abelian groups that
![]() is isomorphic as a
is isomorphic as a
![]() -module to
-module to
![]() , as claimed.
, as claimed.
![]()