For any congruence subgroup 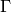 , the direct sum
, the direct sum
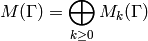
is a ring, since the product of modular forms
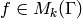 and
and 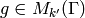 is
an element
is
an element 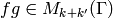 . Sage can compute
likely generators for rings of modular forms, but currently doesn’t
prove any of these results.
. Sage can compute
likely generators for rings of modular forms, but currently doesn’t
prove any of these results.
We verify the statement proved in Serre’s “A Course in Arithmetic”
that 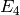 and
and 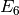 generate the space of level
one modular forms.
generate the space of level
one modular forms.
sage: from sage.modular.modform.find_generators import modform_generators
sage: modform_generators(1)
[(4, 1 + 240*q + 2160*q^2 + 6720*q^3 + O(q^4)),
(6, 1 - 504*q - 16632*q^2 - 122976*q^3 + O(q^4))]
Have you ever wondered which forms generate the ring
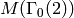 ? it turns out a form of weight 2 and two
forms of weight 4 together generate.
? it turns out a form of weight 2 and two
forms of weight 4 together generate.
sage: modform_generators(2)
[(2, 1 + 24*q + 24*q^2 + ... + 288*q^11 + O(q^12)),
(4, 1 + 240*q^2 + .. + 30240*q^10 + O(q^12)),
(4, q + 8*q^2 + .. + 1332*q^11 + O(q^12))]
Here’s generators for 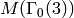 . Notice that
elements of weight
. Notice that
elements of weight 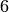 are now required, in addition to
weights
are now required, in addition to
weights 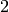 and
and 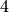 .
.
sage: modform_generators(3)
[(2, 1 + 12*q + 36*q^2 + .. + 168*q^13 + O(q^14)),
(4, 1 + 240*q^3 + 2160*q^6 + 6720*q^9 + 17520*q^12 + O(q^14)),
(4, q + 9*q^2 + 27*q^3 + 73*q^4 + .. + O(q^14)),
(6, q - 6*q^2 + 9*q^3 + 4*q^4 + .. + O(q^14)),
(6, 1 - 504*q^3 - 16632*q^6 .. + O(q^14)),
(6, q + 33*q^2 + 243*q^3 + .. + O(q^14))]