



Next: Endomorphism Rings over Number
Up: Invariants of Modular Abelian
Previous: Invariants of Modular Abelian
Contents
Let 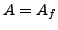 be a modular abelian variety over
be a modular abelian variety over
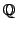 associated to a
newform in
associated to a
newform in
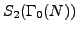 .
Let
.
Let 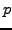 be a prime of good reduction for
be a prime of good reduction for 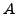 (so
(so 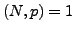 ).
Let
).
Let
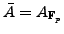 be the reduction of the
be the reduction of the 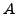 modulo
modulo 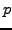 ,
which is an abelian variety over
,
which is an abelian variety over
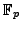 .
.
Problem 8.1.1
Compute the endomorphism ring
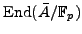
.
The endomorphism ring of
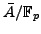 contains
contains
![$ \mathbb{T}[\pi_p] =
\mathbb{Z}[\{\alpha_n\}][\pi_p]$](img333.png) , where
, where 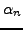 is the
is the 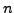 -th coefficient
of the cusp form
-th coefficient
of the cusp form 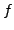 of
of 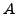 , and the Frobenius endomorphism
, and the Frobenius endomorphism 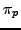 satisfies
satisfies
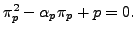 If
If 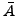 is
ordinary (i.e. has
is
ordinary (i.e. has 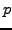 -rank
-rank
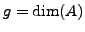 ), then
), then
where
![$ K = \mathbb{T}[\pi_p] \otimes\mathbb{Q}$](img340.png) and
and
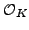 is its maximal
order.
These reductions modulo
is its maximal
order.
These reductions modulo 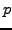 are CM abelian varieties, but in general only
the real subring
are CM abelian varieties, but in general only
the real subring
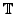 generated by the trace terms lift back
to the modular abelian variety over
generated by the trace terms lift back
to the modular abelian variety over
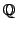 .
.
Note that the invariant
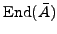 is an invariant of the isomorphism
class, but not the isogeny class, of
is an invariant of the isomorphism
class, but not the isogeny class, of 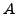 . For instance the isogeny class
of elliptic curves of conductor 57 denoted 57C by Cremona, consists
of two curves:
. For instance the isogeny class
of elliptic curves of conductor 57 denoted 57C by Cremona, consists
of two curves:
such that there exists a 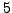 -isogeny
-isogeny
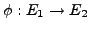 between them.
This induces isogenies on the reductions
between them.
This induces isogenies on the reductions
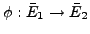 ,
from which one concludes, for each
,
from which one concludes, for each 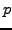 , that either
, that either 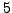 is a split or ramified
prime in
is a split or ramified
prime in
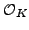 , or that
, or that 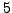 divides the index
divides the index
![$ [\mathcal{O}_K:\mathbb{Z}[\pi_p]]$](img346.png) , and the two
local endomorphism rings differ by index 5:
, and the two
local endomorphism rings differ by index 5:
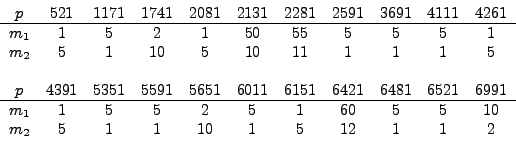
If we consider among the first 1000 primes those for which 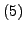 is inert
in
is inert
in
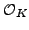 , we can tabulate indices
, we can tabulate indices
![$ m_i = [\mathcal{O}_K:{\mathrm{End}}(\bar{E}_i)]$](img349.png) :
:
The primes for which 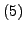 is inert in
is inert in
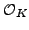 are rare,
and that there is no obvious preference for
are rare,
and that there is no obvious preference for 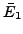 or
or 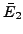 to have
the larger endomorphism ring.
Can one determine a density of primes
to have
the larger endomorphism ring.
Can one determine a density of primes 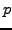 for which
for which 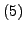 is inert in
is inert in
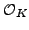 ?
?
Note that the condition
![$ [\mathcal{O}_K:\mathbb{Z}[\pi_p]] \equiv 0 \bmod 5$](img353.png) is equivalent,
up to isomorphism, to the action of
is equivalent,
up to isomorphism, to the action of 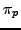 on
on
![$ \bar{E}_i[5]$](img354.png) being:
being:
The additional condition that
![$ [{\mathrm{End}}(\bar{E}):\mathbb{Z}[\pi_p]] \equiv 0 \bmod 5$](img356.png) is
measured by the condition:
is
measured by the condition:
Note that there a similar number of primes of supersingular reduction
among the first 1000 primes, yet they are known to form a set of density zero.
Problem 8.1.2
Implement in
SAGE an algorithm to compute
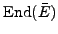
for
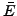
an elliptic curve over a finite field. (Does this problem make sense
for the special fiber of a Néron model as well?)
For higher dimensional modular abelian varieties, it would be
interesting to have algorithms to determine the exact endomorphism
rings at 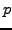 , and to characterize the primes at which the reduction
, and to characterize the primes at which the reduction
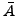 has
has 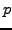 -rank
-rank 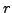 in
in
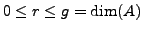 .
.
Problem 8.1.3
Let
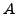
be an abelian variety of dimension
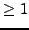
attached
to a newform and let
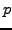
be a prime of good reduction.
Find an algorithm to compute the exact endomorphism
ring
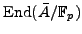
.
Problem 8.1.4
Let
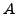
be an abelian variety of dimension
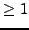
attached
to a newform. Give an algorithm to compute set of primes at
which the reduction
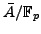
has
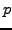
-rank
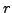
with
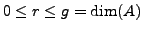
.
Note that the endomorphism rings at ordinary primes are CM orders, and
the canonical lift of the reduction 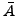 is a CM abelian variety.
A database of invariants of CM moduli for small genus would aid in
classifying these endomorphism rings (at small primes).
is a CM abelian variety.
A database of invariants of CM moduli for small genus would aid in
classifying these endomorphism rings (at small primes).
Problem 8.1.5
Create a database of invariants of CM moduli for small genus.




Next: Endomorphism Rings over Number
Up: Invariants of Modular Abelian
Previous: Invariants of Modular Abelian
Contents
William Stein
2006-10-20
![]() contains
contains
![]() , where
, where ![]() is the
is the ![]() -th coefficient
of the cusp form
-th coefficient
of the cusp form ![]() of
of ![]() , and the Frobenius endomorphism
, and the Frobenius endomorphism ![]() satisfies
satisfies
![]() If
If ![]() is
ordinary (i.e. has
is
ordinary (i.e. has ![]() -rank
-rank
![]() ), then
), then
![]() is an invariant of the isomorphism
class, but not the isogeny class, of
is an invariant of the isomorphism
class, but not the isogeny class, of ![]() . For instance the isogeny class
of elliptic curves of conductor 57 denoted 57C by Cremona, consists
of two curves:
. For instance the isogeny class
of elliptic curves of conductor 57 denoted 57C by Cremona, consists
of two curves:
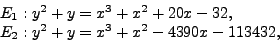
![$\displaystyle \frac{[\mathcal{O}_K:{\mathrm{End}}(\bar{E}_1)]}{[\mathcal{O}_K:{\mathrm{End}}(\bar{E}_2)]} \in \{5^{-1},5\}.
$](img347.png)
![]() is equivalent,
up to isomorphism, to the action of
is equivalent,
up to isomorphism, to the action of ![]() on
on
![]() being:
being:
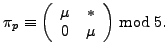
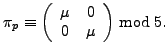
![]() , and to characterize the primes at which the reduction
, and to characterize the primes at which the reduction
![]() has
has ![]() -rank
-rank ![]() in
in
![]() .
.
![]() is a CM abelian variety.
A database of invariants of CM moduli for small genus would aid in
classifying these endomorphism rings (at small primes).
is a CM abelian variety.
A database of invariants of CM moduli for small genus would aid in
classifying these endomorphism rings (at small primes).