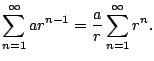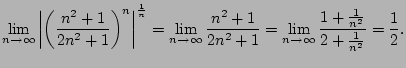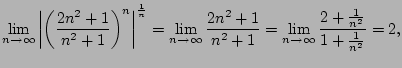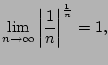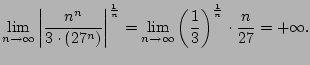Example 6.4.11
Let's apply the root test to
We have
Thus the root test tells us exactly what we already know about
convergence of the geometry series (except when
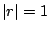
).
Example 6.4.15
Consider
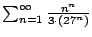
.
To apply the root test, we compute
Again, the limit diverges, as in Example
6.4.8.