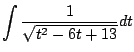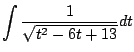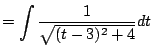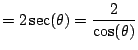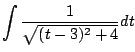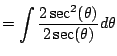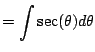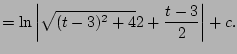Return more midterms?
Rough meaning of grades:
 29-34 is A 29-34 is A
 23-28 is B 23-28 is B
 17-22 is C 17-22 is C
 11-16 is D 11-16 is D
Regarding the quiz--if you do every homework problem that was assigned,
you'll have a severe case of deja vu on the quiz! On the exam, we do
not restrict ourselves like this, but you get to have a sheet of paper. |
The first homework problem is to compute
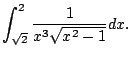 |
(5.4) |
Your first idea might be to do some sort of
substitution, e.g., 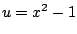 , but
, but 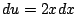 is nowhere to be seen and this simply doesn't work.
Likewise, integration by parts gets us nowhere.
However, a technique called ``inverse trig substitutions''
and a trig identity easily dispenses with the
above integral and several similar ones!
Here's the crucial table:
is nowhere to be seen and this simply doesn't work.
Likewise, integration by parts gets us nowhere.
However, a technique called ``inverse trig substitutions''
and a trig identity easily dispenses with the
above integral and several similar ones!
Here's the crucial table:
| Expression |
Inverse Substitution |
Relevant Trig Identity |
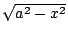 |
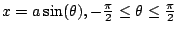 |
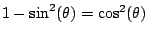 |
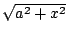 |
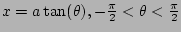 |
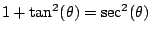 |
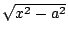 |
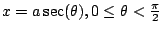 or or
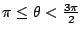 |
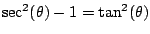 |
Inverse substitution works as follows. If we write 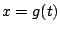 , then
, then
This is not the same as substitution. You can just apply
inverse substitution to any integral directly--usually you get
something even worse, but for the integrals in this section using
a substitution can vastly improve the situation.
If  is a
is a  function, then you can even use inverse substitution
for a definite integral. The limits of integration are obtained as follows.
function, then you can even use inverse substitution
for a definite integral. The limits of integration are obtained as follows.
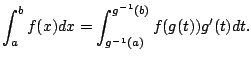 |
(5.5) |
To help you understand this, note that as 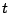 varies from
varies from
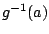 to
to 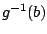 , the function
, the function 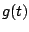 varies
from
varies
from
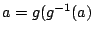 to
to
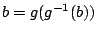 , so
, so 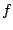 is being integrated
over exactly the same values. Note also that (5.3.2) once
again illustrates Leibniz's brilliance in designing the notation
for calculus.
is being integrated
over exactly the same values. Note also that (5.3.2) once
again illustrates Leibniz's brilliance in designing the notation
for calculus.
Let's give it a shot with (5.3.1).
From the table we use the inverse substition
We get
Wow! That was like magic. This is really an amazing technique.
Let's use it again to find the area of an ellipse.
Example 5.3.1
Consider an ellipse with radii
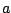
and
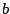
, so it
goes through
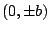
and
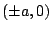
. An equation
for the part of an ellipse in the first quadrant is
Thus the area of the entire ellipse is
The
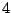
is because the integral computes
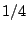
th of the area
of the whole ellipse.
So we need to compute
Obvious substitution with
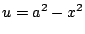
...? nope. Integration by parts...? nope.
Let's try inverse substitution.
The table above suggests using
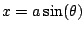 , so
, so
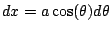 .
We get
.
We get
Thus the area is
Consistency Check: If the ellipse is a circle, i.e.,
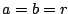
, this is
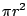
,
which is a well-known formula for the area of a circle.
Remark 5.3.2
Trigonometric substitution is useful for functions that
involve
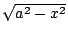
,
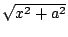
,
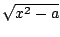
,
but
not all at once!. See the above table for how
to do each.
One other important technique is to use completing the square.
Example 5.3.3
Compute
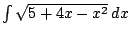
.
We
complete the square:
Thus
We do a usual substitution to get rid of the
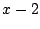
.
Let
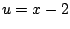
, so
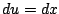
.
Then
Now we have an integral that we can do; it's almost
identical to the previous example, but with
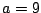
(and this is an indefinite integral).
Let
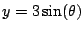
, so
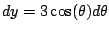
.
Then
Of course, we
must transform back into a function in
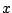
, and
that's a little tricky.
Use that
so that
Here we use that
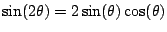
.
Also, to compute
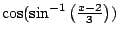
, we
draw a right triangle with side lengths
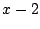
and
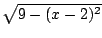
,
and hypotenuse
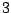
.
Example 5.3.4
Compute
To compute this, we complete the square, etc.
[[Draw triangle with sides
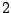
and
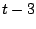
and
hypotenuse
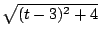
.
Then
Back to the integral, we have
William Stein
2006-03-15
![]() , then
, then
![]() is a
is a ![]() function, then you can even use inverse substitution
for a definite integral. The limits of integration are obtained as follows.
function, then you can even use inverse substitution
for a definite integral. The limits of integration are obtained as follows.
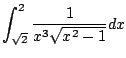
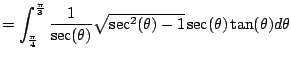
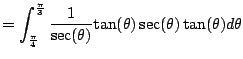
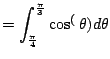
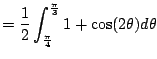
![$\displaystyle = \frac{1}{2} \left[ \theta + \frac{1}{2}\sin(2\theta)\right]_{\frac{\pi}{4}}^{\frac{\pi}{3}}$](img643.png)
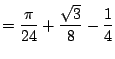
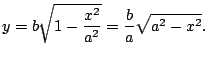
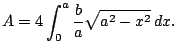
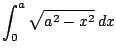
![]() , so
, so
![]() .
We get
.
We get
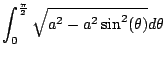
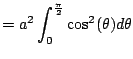
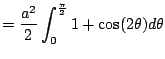
![$\displaystyle = \frac{a^2}{2}\left[ \theta + \frac{1}{2}\sin(2\theta) \right]_0^{\frac{\pi}{2}}$](img658.png)
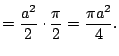
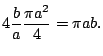
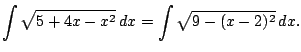
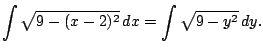
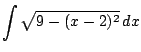
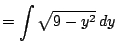
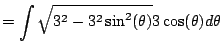
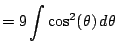
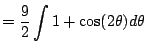
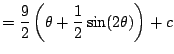
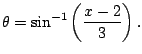
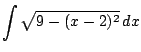
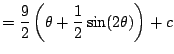
![$\displaystyle =\frac{9}{2} \left[\sin^{-1}\left(\frac{x-2}{3}\right) + \sin(\theta)\cos(\theta) \right] + c$](img684.png)
![$\displaystyle =\frac{9}{2} \left[\sin^{-1}\left(\frac{x-2}{3}\right) + \left(\frac{x-2}{3}\right) \cdot \left(\frac{\sqrt{9-(x-2)^2}}{3}\right) \right] + c.$](img685.png)