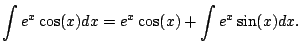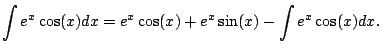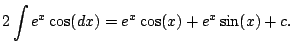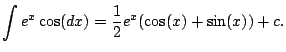Quiz next Friday
Today: 7.1: integration by parts
Next: 7.2: trigonometric integrals
and supplement 2-functions with complex values
Exams: Average 19.68 (out of 34).
Tetrahedron problem:
(The function that gives the base of the triangle
cross section is a linear function that is 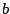 at at 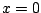 and 0 at
and 0 at 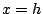 , which allows you to easily determine
it without thinking about geometry.) , which allows you to easily determine
it without thinking about geometry.)
|
| Differentiation |
Integration |
| Chain Rule |
Substitution |
| Product Rule |
Integration by Parts |
The product rule is that
Integrating both sides leads to a new fundamental technique
for integration:
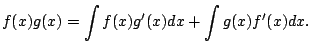 |
(5.1) |
Now rewrite (5.1.1) as
Shorthand notation:
Then have
So what! But what's the big deal?
Integration by parts is a fundamental technique of integration. It
is also a key step in the proof of many theorems
in calculus.
Example 5.1.1
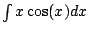
.
We get
``Did this do anything for us?'' Indeed, it did.
Wait a minute--how did we know to pick 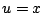 and
and 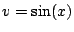 ? We could have picked them
other way around and still written down true statements.
Let's try that:
? We could have picked them
other way around and still written down true statements.
Let's try that:
Did this help!? NO. Integrating
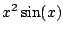
is harder
than integrating
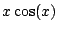
. This formula is completely correct,
but is hampered by being useless in this case.
So how
do you pick them?
Choose the 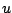 so that
when you differentiate it you get something simpler;
when you pick
so that
when you differentiate it you get something simpler;
when you pick 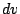 , try to choose something whose
antiderivative is simpler.
, try to choose something whose
antiderivative is simpler.
Sometimes you have to try more than once. But with
a good eraser nodoby will know that it took you two
tries.
Question 5.1.2
If integration by parts once is good, then sometimes twice is
even better? Yes, in some examples (see Example
5.1.5).
But in the above example, you just undo what you did and basically
end up where you started, or you get something even worse.
Example 5.1.3
Compute
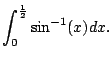
Two points:
- It's a definite integral.
- There is only one function; would you think to do
integration by parts? But it is a product; it just
doesn't look like it at first glance.
Your choice is made for you, since we'd be back where
we started if we put
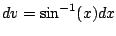 .
.
We get
Now we use substitution with
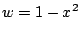
,
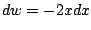
, hence
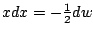
.
Hence
But shouldn't we change the limits because we did a substitution?
(No, since we computed the indefinite integral and put it back;
this time we did the other option.)
Is there another way to do this? I don't know. But for
any integral, there might be several different techniques.
If you can think of any other way to guess an antiderivative,
do it; you can always differentiate as a check.
Note: Integration by parts is tailored toward doing indefinite
integrals.
Example 5.1.4
This example illustrates how to use integration by parts twice.
We compute
We have
Did this help? It helped, but it did
not finish
the integral off. However, we can deal with the remaining
integral, again using integration by parts.
If you do it twice, you
what to keep going in the same
direction. Do not switch your choice, or you'll undo
what you just did.
Now putting this above, we have
Do you think you might have to do integration by parts three times?
What if it were
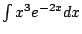 ? Grrr - you'd have to do it
three times.
? Grrr - you'd have to do it
three times.
Example 5.1.5
Compute
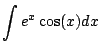 .
.
Which should be
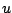
and which should be
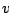
? Taking the derivatives
of each type of function does not change the type. As a practical
matter, it doesn't matter. Which would you
prefer to find the
antiderivative of? (Both choices work, as long as you keep going in
the same direction when you do the second step.)
We get
We have to do it again. This time we choose (going in the
same direction):
We get
Did we get anywhere? Yes! No! First impression: all this work,
and we're back where we started from! Yuck. Clearly we don't want
to integrate by parts yet again.
BUT.
Notice the
minus sign in front of
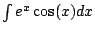
;
You can add the integral to both sides and get
Hence
William Stein
2006-03-15
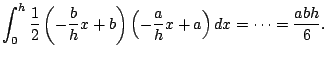
![$\displaystyle \frac{d}{dx}\left[ f(x) g(x)\right] = f(x) g'(x) + f'(x) g(x).
$](img476.png)
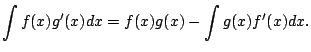
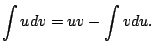
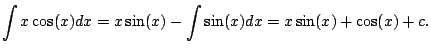
![]() and
and ![]() ? We could have picked them
other way around and still written down true statements.
Let's try that:
? We could have picked them
other way around and still written down true statements.
Let's try that:
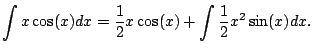
so that when you differentiate it you get something simpler; when you pick
, try to choose something whose antiderivative is simpler.
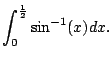 Two points:
Two points:
![]() .
.
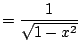
![$\displaystyle \int_0^{\frac{1}{2}} \sin^{-1}(x) dx
= \left[x\sin^{-1}(x)\right]_0^{\frac{1}{2}}
- \int_0^{\frac{1}{2}} \frac{x}{\sqrt{1-x^2}} dx.
$](img509.png)
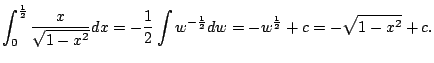
![$\displaystyle \int_0^{\frac{1}{2}} \sin^{-1}(x) dx
= \left[x\sin^{-1}(x)\right]...
... \sqrt{1-x^2}\right]^{\frac{1}{2}}_0
= \frac{\pi}{12} + \frac{\sqrt{3}}{2} - 1
$](img514.png)
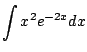
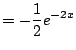
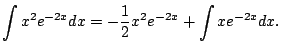
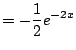
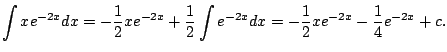
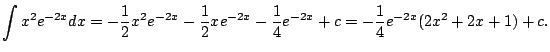
![]() ? Grrr - you'd have to do it
three times.
? Grrr - you'd have to do it
three times.
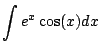 .
Which should be
.
Which should be