Physical Intuition

In the previous lecture we mentioned a relation between velocity, distance, and the meaning of integration, which gave you a physical way of thinking about integration. In this section we generalize our previous observation.

The following is a restatement of the fundamental theorem of calculus:

Theorem 2.2.6 (Net Change Theorem)   The definite integral of the rate of change $F'(x)$ of some quantity $F(x)$ is the net change in that quantity:

$$\int_{a}^b F'(x) dx = F(b) - F(a).$$

For example, if $p(t)$ is the population of students at UCSD at time $t$, then $p'(t)$ is the rate of change. Lately $p'(t)$ has been positive since $p(t)$ is growing (rapidly!). The net change interpretation of integration is that

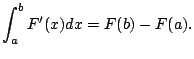
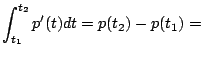$$\int_{t_1}^{t_2} p'(t) dt = p(t_2) - p(t_1) =$$    change in number of students from time $t_1$ to $t_2$$$.$$

Another very common example you'll seen in problems involves water flow into or out of something. If the volume of water in your bathtub is $V(t)$ gallons at time $t$ (in seconds), then the rate at which your tub is draining is $V'(t)$ gallons per second. If you have the geekiest drain imaginable, it prints out the drainage rate $V'(t)$. You can use that printout to determine how much water drained out from time $t_1$ to $t_2$:

$$\int_{t_1}^{t_2} V'(t) dt =$$$$\text { water that drained out from time $t_1$ to $t_2$ }$$

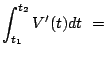
Some problems will try to confuse you with different notions of change. A standard example is that if a car has velocity $v(t)$, and you drive forward, then slam it in reverse and drive backward to where you start (say 10 seconds total elapse), then $v(t)$ is positive some of the time and negative some of the time. The integral $\int_{0}^{10} v(t) dt$ is not the total distance registered on your odometer, since $v(t)$ is partly positive and partly negative. If you want to express how far you actually drove going back and forth, compute $\int_{0}^{10} \vert v(t)\vert dt$. The following example emphasizes this distinction:

Example 2.2.7   An ancient dragon is pacing on the cliffs in Del Mar, and has velocity $v(t)=t^2-2t-8$. Find (1) the displacement of the dragon from time $t=1$ until time $t=6$ (i.e., how far the dragon is at time $6$ from where it was at time $1$), and (2) the total distance the dragon paced from time $t=1$ to $t=6$.

For (1), we compute

$$\int_{1}^6 (t^2 - 2t - 8) dt = \left[ \frac{1}{3} t^3 - t^2 - 8t \right]_{1}^6 = - \frac{10}{3}.$$

For (2), we compute the integral of $\vert v(t)\vert$:

$$\int_{1}^6 \vert t^2 - 2t - 8\vert dt = \left[ -\left(\frac{1}{3}... ...t[ \frac{1}{3} t^3 - t^2 - 8t \right]_{4}^6 = 18 + \frac{44}{3} = \frac{98}{3}.$$